Are Three Eyes Better Than Two?
By David Abercrombie, Mentor Graphics
Error analysis in triple patterning is challenging, but a pyramid approach helps designers prioritize and eliminate errors without triggering new ones
It is clear that having two eyes is better than having just one. Not only is depth perception much better, but we get to enjoy 3D movies because of it. There is also some sense of security in knowing that if something terrible happened to one eye, you always have a backup.
Have you ever wondered if these sorts of advantages are extendable? You’ve probably heard the phrase about someone having a “third eye in the back of their head” due to their ability to detect something happening behind them. As useful as it sounds, I am sure that despite the potential benefits, having a third eye would also introduce some complexity and potential confusion.
In this blog I wanted to spend some time talking about error visualization in triple-patterning (TP). Strangely enough, this topic does share some common themes with the discussion of the benefits and challenges of having three eyes.
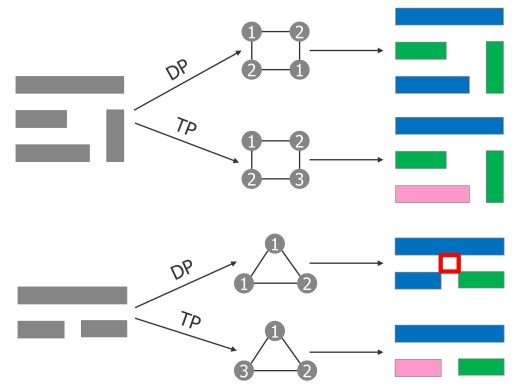
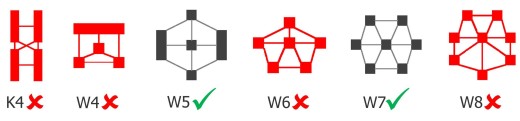
First, the good news. Just as having an extra eye in the back of your head might help you detect more things going on around you, adding a third color in mask decomposition also helps resolve many problems. Figure 1 shows how having the third color in TP helps overcome the odd cycle problem in double-patterning (DP).
Figure 1: Comparing odd and even cycle decomposition in double & triple patterning.
An even cycle of critically spaced polygons as shown in the top illustration of Figure 1 is legally decomposable in either DP or TP. An off cycle of critically spaced polygons like the bottom example is not legally decomposable in DP—but it is legally decomposable in TP simply because there is an extra color to use. So, TP is able to decompose many more layout constructs in general than DP. However, not everything is decomposable with TP either and just as with DP we need some way to provide meaningful error markers to help designers with constructs that are not decomposable. In DP we had the odd cycle “ring” shown in Figure 1. It essentially maps the inner circle of critically spaced polygons that form the odd cycle. The ring makes a useful error marker for the designer because you can quickly see how the cycle is formed and the multiple spacing changes that you could pick from to break the cycle.
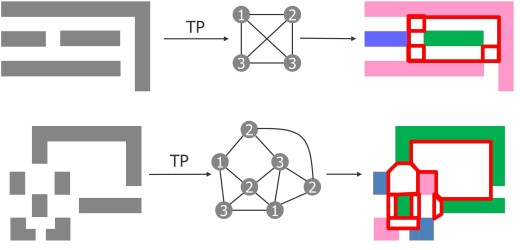
In TP there is nothing as simple as odd vs. even cycles when it comes to the decomposability of layout constructs. Any simple even or odd cycle is decomposable. Only, much more complicated constructs are not decomposable in TP. Figure 2 shows some examples of such constructs.
Figure 2: Examples of layout constructs that are not decomposable in TP.
You can see that these constructs are not just simple odd or even cycles of critically spaced polygons. Because of the complexity of the constructs, you can see that trying to draw the inner circle of critically spaced polygons, as shown in Figure 2, does not provide a very useful tool for the designer.
Although TP offers the advantage of successfully decomposing many more layout constructs, error visualization of non-decomposable constructs is much more complicated. Because of this we have had to do extensive analysis of just what type of errors occur in TP designs and approach the problem of visualization a little differently to make it useful for designers. We have found that there is no one-size-fits-all kind of error visualization for TP.
We have approached the problem differently for TP. There are several classes of issues that occur in typical designs and we found that one type of error can trigger other types to occur, which leads to an incredible amount of “noise” in the error output. It was difficult for a designer to find where to focus fixing efforts with all the noise. I can imagine a third eye may have the same problem.
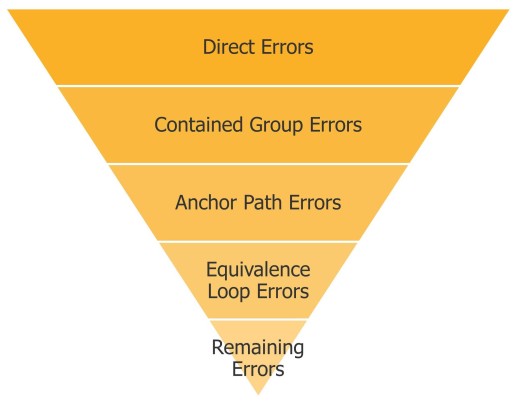
To solve this problem, we created a sort of inverted pyramid approach to error visualization in TP. Essentially, we find the “smallest” kinds of errors first and filter them out of the graph so that they don’t trigger additional types of errors. Then we find the next “smallest” type of error remaining and so forth. By “smallest” I mean an error which can be explained in the smallest collection of polygons. It’s like a backwards sift. The smallest errors are sifted out first, leaving fewer of the next larger error types until nothing is left. Figure 3 shows this inverted pyramid sifted error concept.
Figure 3: Inverted pyramid sifted error approach to TP error visualization.
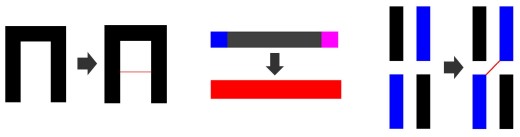
Let’s look at each level of the pyramid more closely. We refer to the smallest (i.e. most compact) form of errors that can exist in a TP design as direct errors. They are direct in that they only involve a single polygon or a single adjacent neighbor. There are three basic situations that can create a direct error, as demonstrated in Figure 4.
Figure 4: Example direct errors in TP layout.
The first situation is when two faces of the same polygon are within a critical distance of each other. This critical spacing requires that the different faces be on different colors, but since both faces belong to the same polygon, only one color is possible. The error is marked by showing the critical spacing constraint between the two edges of the same polygon.
The second situation is when two or more different anchor color constraints (a portion of the layout pre-assigned to a given color) are applied to the same polygon (i.e. two parts of the same polygon pre-assigned to different colors). Again, in individual polygon can only have one color so all these anchoring constraints cannot both be honored. The error is marked by showing the polygon with multiple anchor constraints.
The third situation is when two critically spaced polygons are both anchored to the same color. Since they are both anchored to the same color they both have to be the same color, but since they are critically spaced they also have to be on different colors. Obviously, both constraints cannot simultaneously be met. The error is marked by showing the critical spacing constraint between the two same anchored polygons.
These error types are found first and put onto their own unique result layer so the designer knows exactly what type of situation is causing them. Then these errors are removed from the analysis of colorability so that no larger error form that they may induce will be detected. This is the sifting process.
The next level of error in the pyramid we call contained group errors. These are compact groups of polygons that have a high degree of critical spacing requirements between them such that three colors cannot satisfy all the constraints. They are a set of well-known and pre-described constructs, which are shown in Figure 5.
Figure 5: Example contained group errors in TP layout.
These pre-described constructs have specific classification, as shown in the labels in Figure 5. The first one is called a k4 complete graph. It consists of a set of four polygons in which each polygon in the set has critical spacing constraints to every other polygon in the set requiring that each polygon cannot be any of the colors of the other three. As there are only three colors, you cannot meet this requirement. The other forms are of a “wheel” classification. They are a set of polygons in which the one in the middle has critical spacing constraints to all the outer polygons and the outer polygons form a ring of critical spacing color constraints. If the outer ring of polygons is an odd number then all three colors will be utilized in coloring the outer ring, leaving no color options for the one in the middle. So a wheel made of 4, 6, 8, etc. cannot be colored. But a wheel of 5, 7, 9, etc. can be colored.
The error marker for each illegal construct shows the entire set of polygons and critical spacing constraints that make it up. If any single critical spacing constraint in the set is removed (i.e. increase the space between the two polygons sufficiently to remove the constraint) then the entire set becomes colorable. So the designer has many different ways in which any single one of these errors can be fixed, providing significant flexibility for resolving the error with as little impact on design area as possible.
Again, these errors trigger larger error types, they are removed from the analysis before searching for the next level of error in the pyramid. The basis for this sifting is that once you fix this compact error, the larger error it creates will also probably be corrected.
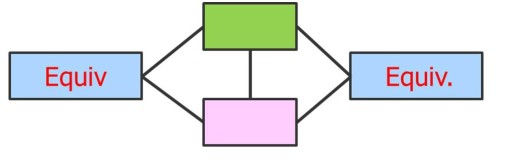
The next two levels of errors in the pyramid are all based on a critical layout construct that occurs frequently in TP design. It is important to understand this construct and its impact on coloring before proceeding. We refer to this critical layout structure as a “diamond equivalence,” and it is illustrated in Figure 6.
Figure 6: Example diamond equivalence structure in TP layout.
This construct consist of four polygons with a particular set of critical spacing constraints. The two polygons in the middle have a critical spacing constraint between them requiring that they be on two different colors. The other two polygons have critical spacing constraints to both of the two polygons in the middle. Since the two middle polygons have used two of the colors already, both of these polygons on the ends must be the third, same, color. It forms a sort of diamond shape in which the two tips of the diamond are force to be equivalent colors. It is also not uncommon in TP layout for a chain of diamond constructs to be created. All the diamond tips in the chain would have to be the same color in such a configuration. Now by itself there is no issue coloring an individual or chain of diamonds. However, they can lead to a few particular problem scenarios that make up the next two levels in the error-sifting pyramid.
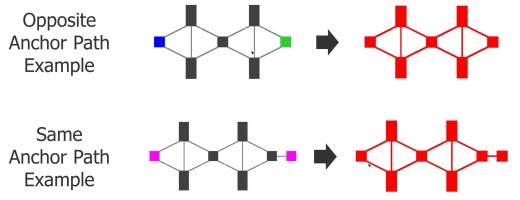
The next level in the pyramid contains what we call anchor path errors. They are chains of diamond constructs that interact with anchored polygons, as shown in Figure 7.
Figure 7: Example anchor path errors in TP layout.
There are two forms of this error type. In the first, a chain of diamond constructs is anchored at one end as one color and anchored on the other end as another color. Since all the tips in the chain are forced to be the same color by the diamond configurations both of these anchor constraints cannot simultaneously be met.
In the other form of the error, a chain of diamond constructs is anchored on one end and the other end has a critical spacing constraint to a polygon that is also anchored to that same color. Since all the tips of the diamonds have to be the same color, the critical spacing color difference to the last anchor cannot be met.
In either case, the error is marked by showing the complete set of polygons and critical spacing constraints that make up the diamond paths between the anchors. Each of these is put onto a separate output layer so the designer can understand the situation causing the error. Removing any single critical spacing constraint in the construct will resolve the coloring issue for the whole construct. Again all of these errors are removed from the analysis before searching for the next level of errors in the layout.
The next level of the pyramid also involves these diamond constructs but doesn’t involve any color anchors. Instead, the diamonds or chains of diamonds form loops back upon themselves, as shown in Figure 8.
Figure 8: Example standard cell library architecture on density balancing.
The polygons that make up the ends of the diamond chains have a critical spacing constraint between them. Since all the tips in the diamond chain have to be the same color, this critical spacing color difference cannot be satisfied.
Again, these errors are output on their own result layer so the designer can distinguish them. Their markers are also the complete set of polygons and critical spacing constraints that make them up. Removing any single critical spacing constraint will fix coloring for the entire set. And finally, these errors are removed from the analysis before searching for additional errors in the next level of the pyramid.
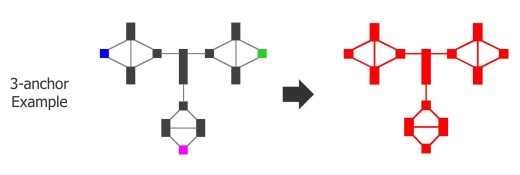
I hope it is clear by now that the approach is to find specific forms of errors starting from the most concise and deliver them on separate output layers for the designer so that he or she understands the specific type of issue that has occurred. By sifting from one level of error type to the other a tremendous amount of noise is removed from the entire system, helping the designer stay focused. By working with customers on real layouts we have identified this set of commonly occurring errors to sift and present. We have found that this set of error types covers every real design issue we have seen to date. However, the list of error types that theoretically could be drawn is much longer and not fully known. So to protect against the occurrence of an error type other than the set shown there is one last level to the pyramid. This level is referred to as remaining errors. Essentially, this is any configuration of polygons and critical spacing constraints that cannot be colored and was not already explained by the previous set of error types. Figure 9 shows an example of an error that could possibly occur and does not fall into one of the previous mentioned categories.
Figure 9: Example TP error that does not fall into one of the previous categories.
The example involves diamonds and anchors, but unlike the anchor path errors shown earlier, more than two anchors and more than a single path are involved. Each of the three diamonds is anchored on one end to a different color. The other end of each diamond is a critical spacing distance from the lone polygon in the middle. These diamond tips would use up all the three colors leaving no legal color for the middle polygon. If any one of the anchors was not present then the middle polygon could be that color. The coloring is not possible only because all three anchors occur and all enforce their color constraint on the middle polygon simultaneously through their diamonds. We have never seen this happen in a real design, but theoretically it could and if it does we would mark the entire set of polygons and critical spacing constraints out on this remaining error layer. If we find that any such particular form of error becomes a common occurrence in real TP designs, we can easily extend the pyramid to make a new specific output layer for it and sift it from the remaining errors.
So having three colors, like having three eyes, brings additional capabilities but also additional complexity. We think that this creative sifted pyramid approach to visualizing TP errors will maximize the designer’s productivity in resolving them.
In my next blog we will take a step back to DP and look at some common error situations that can occur in place and route design environments and some best practice strategies for addressing them.
Author
David Abercrombie is the advanced physical verification methodology program manager at Mentor Graphics.
Liked this article? Then how about this –
Mentor Graphics Multi-Patterning Solutions
This article was originally published on www.semiengineering.com