Multi-stage cyclic symmetry in rotor dynamics
For industrial gas turbines and jet engines, it is almost impossible to work with full 3D models. So, to do simulation, you must rely on intelligent model reduction techniques. Multi-stage cyclic symmetry for rotor dynamics in Simcenter 3D extends classic symmetry-based reduction solutions to the application of having multiple rotors with different numbers of sectors side-by-side.
Complex rotor dynamics for large turbomachinery
There are only a few engineering domains in which poorly executed or inaccurate simulations literally endanger lives. But as we wrote in a previous blog, for rotor dynamics this is certainly the case. Rotating machinery are the vital organs of a mechanical product. They make the mechanism do what it needs to do. They are places where important functional energy conversions take place and hence where a lot of energy is concentrated. A failure in a spinning rotor usually happens with a lot of drama. Think of aircraft jet engines, or even cardiac pumps as examples. These machines just can’t have unscheduled shutdowns.
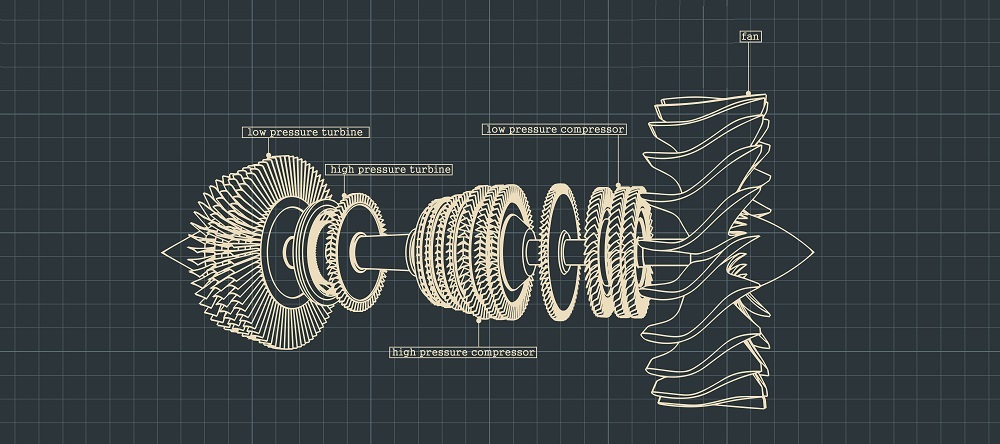
Simulating rotor dynamics is challenging, however, as rotating equipment can be very complex. This is especially the case for turbomachinery such as gas turbines and jet engines for industrial applications. For calculations to be accurate, you need to take an enormous number of small details into account. And as the structures themselves often have quite large dimensions, this means that models of the entire structure in 3D can become enormous and are almost impossible to work with.
Reducing model size by using axisymmetry
Fortunately, there are also a lot of methodologies to reduce model size while keeping accuracy. We already explained in another blog how you can gain enormous time savings by making use of axisymmetry. We demonstrated how this is possible in Simcenter 3D for Rotor Dynamics. However, there is one particularity we did not address.
More complex structures like, for example, gas turbines and jet engines, include several rotors made of different stages, one after the other, especially in their compressor part. Those are not axisymmetric but show symmetry in the sense of cyclic symmetry, where you can identify and isolate a sector, and then reproduce it around the rotor axis. However, the successive stages do not necessarily have the same number of sectors. For such cases, the classic formulation for cyclic symmetry in rotor dynamics requires an extension. The video below shows a typical example.
Multi-stage cyclic symmetry for rotor dynamics
These are no exotic cases of course. On the contrary. In industrial applications, multiple stages are the rule rather than the exception. But for simulation, this is yet another layer of complexity that requires very special technology.
The method we propose delivers unmatched solution speed at no cost of accuracy. It has been developed within the framework of ICOGEN (Integration of COmposites for Greener Engine), a public-funded research project. The objective of the project, carried out in collaboration with Safran Aero Boosters, was to predict the modal and dynamic response of a rotating bladed drum compressor. The case was already extensively described in a blog post as well.
So, what’s new? The method is now fully available in Simcenter 3D for Rotor Dynamics.
Multi-stage cyclic symmetry in Simcenter 3D
The typical complexities that arise when you want to exploit cyclic symmetry for multi-stage models are that meshes are not compatible from one stage to another, and that the model needs to describe properly what happens at the junction. For the latter aspect, we just need to remember that on both sides, the behavior of the sectors is described by a (albeit different) combination of harmonics. If we want to achieve displacement compatibility and force equilibrium at the junction, we need to make sure that there is continuity in the wave propagations. To do so, the solver will check which harmonics are active on both sides, and automatically add those that are necessary to make a smooth transition. The method has been subject to research many times.[1][2]
You can complete the entire workflow in Simcenter 3D 2022.1, from the modeling of the sectors, to the definition of the inter-stage junction, to the recombination of results across the sectors of the various stages and the added harmonics. The multi-stage cyclic symmetry capability has been added to the Simcenter Nastran SOL414 solution.
Demo example multi-stage cyclic symmetry
In the video below, you can see an example of how multi-stage cyclic symmetry works in Simcenter 3D for Rotor Dynamics.
We study a case of 3 stages in a bladed drum compressor, all having a different number of sectors. To define each interstage junction, we select adjacent elements of the corresponding sectors. So, in this case, we need to do this two times.
The reduced model that we create in this way supports any type of analysis: static, nonlinear transient response, or as in this video, in complex modal analysis to compute a Campbell diagram. In this example, we calculate 2-diameters modes, with wavenumber 2, and we define the rotation speed range.
When looking at the results, we can plot a Campbell diagram and we can visualize the mode shapes on individual sectors. Or we can recombine the results on the full 3D model. You can then also see that the interstage junction has been properly taken into consideration.
Conclusion
Simcenter 3D includes the full workflow and solver technology to accurately and efficiently calculate the rotor dynamics behavior for large industrial cases of gas turbines and jet engines.
With Simcenter 3D 2022.1, we are taking the next step to let you deal with even more complexity than ever before, and this even faster than ever before.
References
- [1] Kill, Norbert. (2008). Application of multi-stage cyclic symmetry to rotor dynamics. Institution of Mechanical Engineers – 9th International Conference on Vibrations in Rotating Machinery. 1. 267-275.
- [2] Kill, Norbert & D’Ambrosio, Flavio. (2018). Extension of the multi-stage cyclic symmetry methodology and application to modal and dynamic response analyses.


