How to Reduce the Complexity of Formal Analysis – Part 4 – Counter Abstraction
When big counters and memories are in the active logic cone of an assertion that keeps coming up as “inconclusive”, they are probably the root cause for inconclusive result. Why? Because the math behind formal algorithms struggles to accommodate very large state spaces; and counters and memories both can introduce a lot of state bits and sequential depth for formal to try to swallow. Fortunately, there are techniques that can help: we can either reduce the size of these elements, or replace them with abstract models. This post will focus on handling counters effectively with formal (dealing with memories will be addressed in Part 5)
For starters, when helping formal digest a counter, set the counter to an ‘X’ value for its initial state instead of ‘0’, and let formal consider all potential values for initial state. This gives the formal algorithms the freedom of action they prefer when they form and solve their equations under-the-hood. Here is an example of how to set a counter’s initial value to ‘X’ in Questa PropCheck:
Note that this tool command will electronically overwrite the RTL reset value without changing your RTL code.
The best part of this technique from an end-user perspective is that when the given property is proven, the proof is valid for the original counter value, and for all time. Conversely, if a counter example (CEX) is found for the property, the CEX would probably be much shorter and easier to interpret than if you used the original counter initialization value. The caveat is that while the “firing” may be not be a design bug, per se – the design might require the counter to always start from ‘0’. Again, if this the case, this ‘X’ method is not useful and other techniques need to be tried.
Another popular and effective way to handle big counters is to replace them with a small state machine model that only considers the critical values of the counter that would trigger interesting design actions. For example, suppose value ‘m’, ‘n-1’ and ‘n’ of the counter are critical. Consider the following state machine as a replacement:
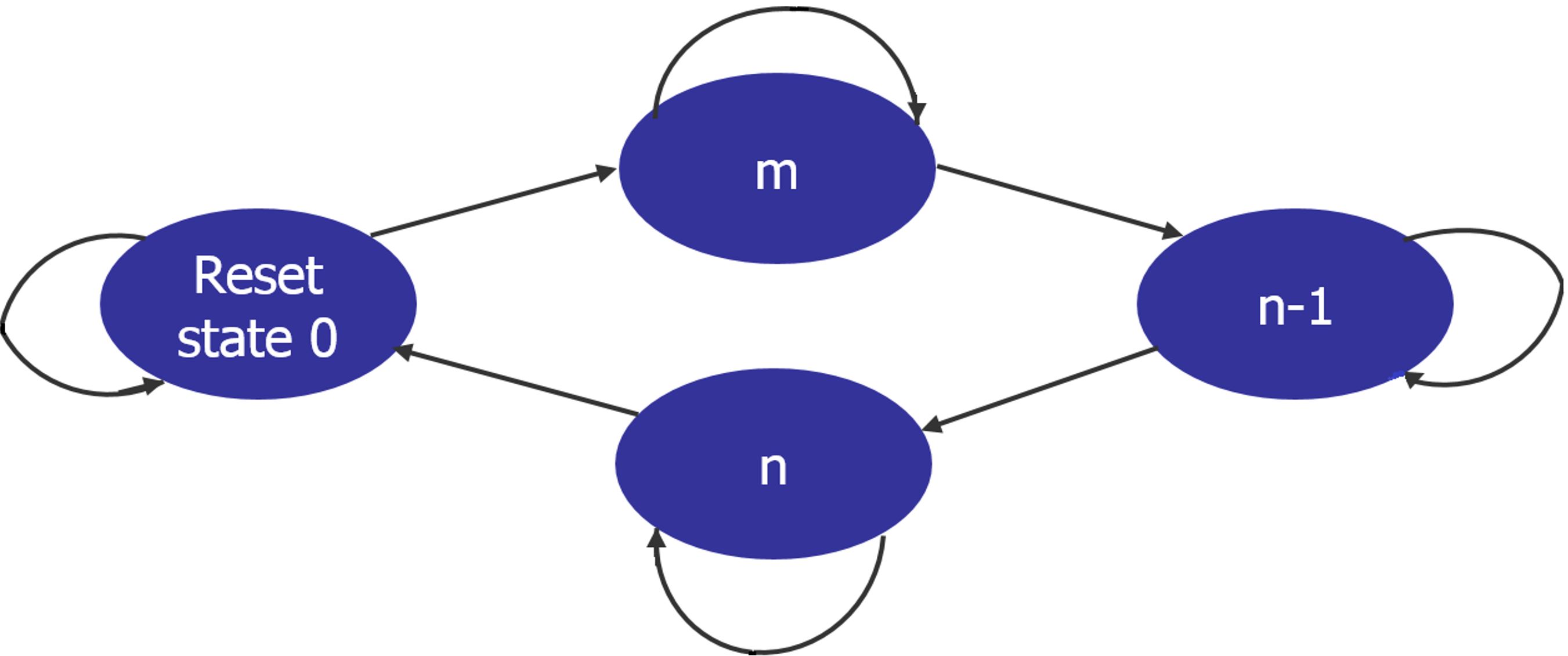
To replace the original counter with this abstract model, we first temporarily bypass/disable the real design’s driving logic – without altering the source RTL in any way – by electronically “cutting” the original counter signal with the tool command “netlist cutpoint” to make it a free variable and then add constraints to it. Since this abstracted counter has only 4 states — much less than the original — the formal engines will be able to reach interesting design states much faster!
Here is an example.
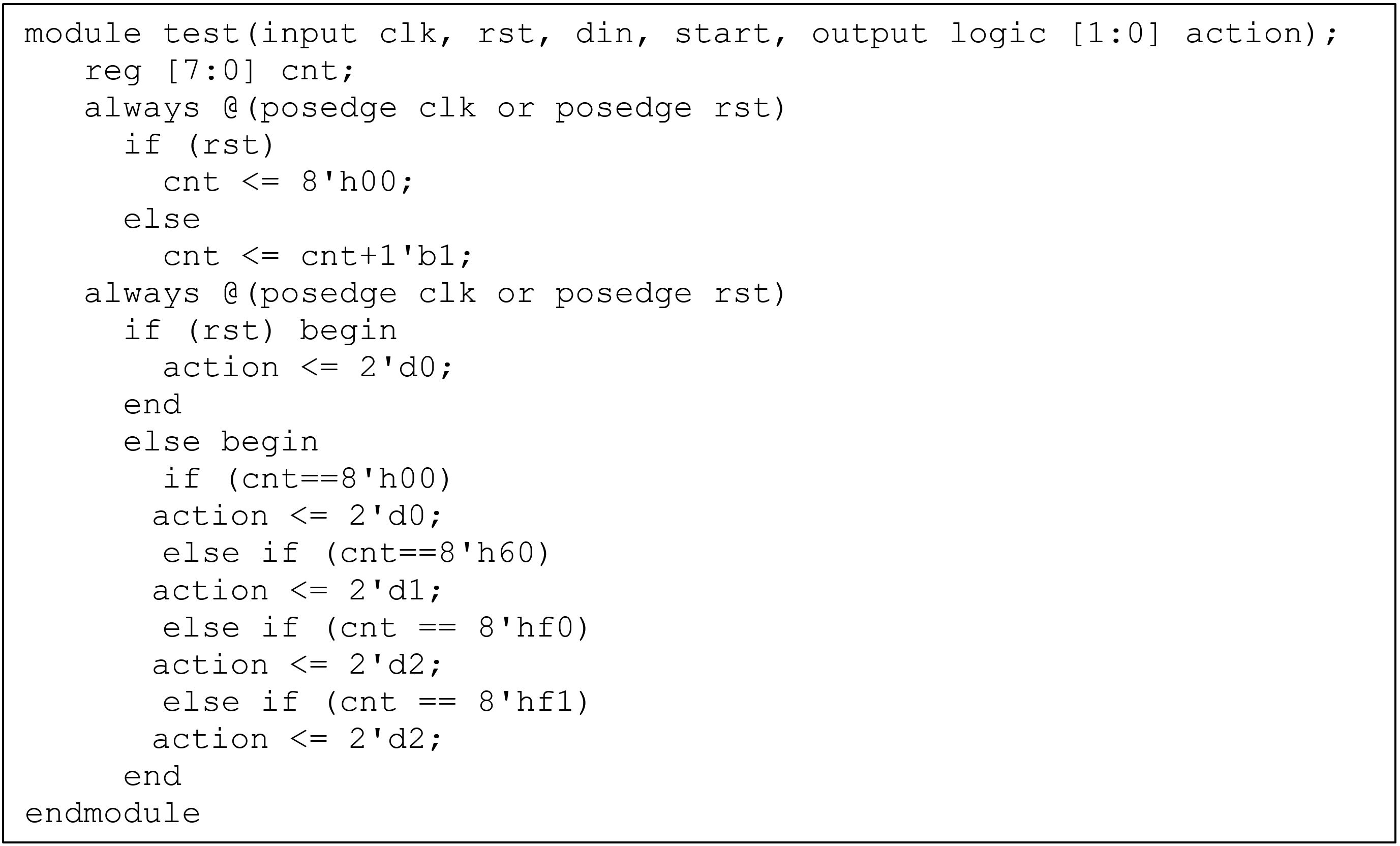
The Makefile to run the test is as follows. The “abs_cnt.do” contains the TCL commands to define the abstract counter for “cnt” in the design. The assertion “assert_action3” should be fired due to the error in RTL that drives “action” to be 2’d2 when “cnt==8’hf1”.
The “abs_cnt.do” file is as follows.
The error trace from using abstract counter is as follows. The firing happened at cycle 4 that is short and easy for debugging the problem.
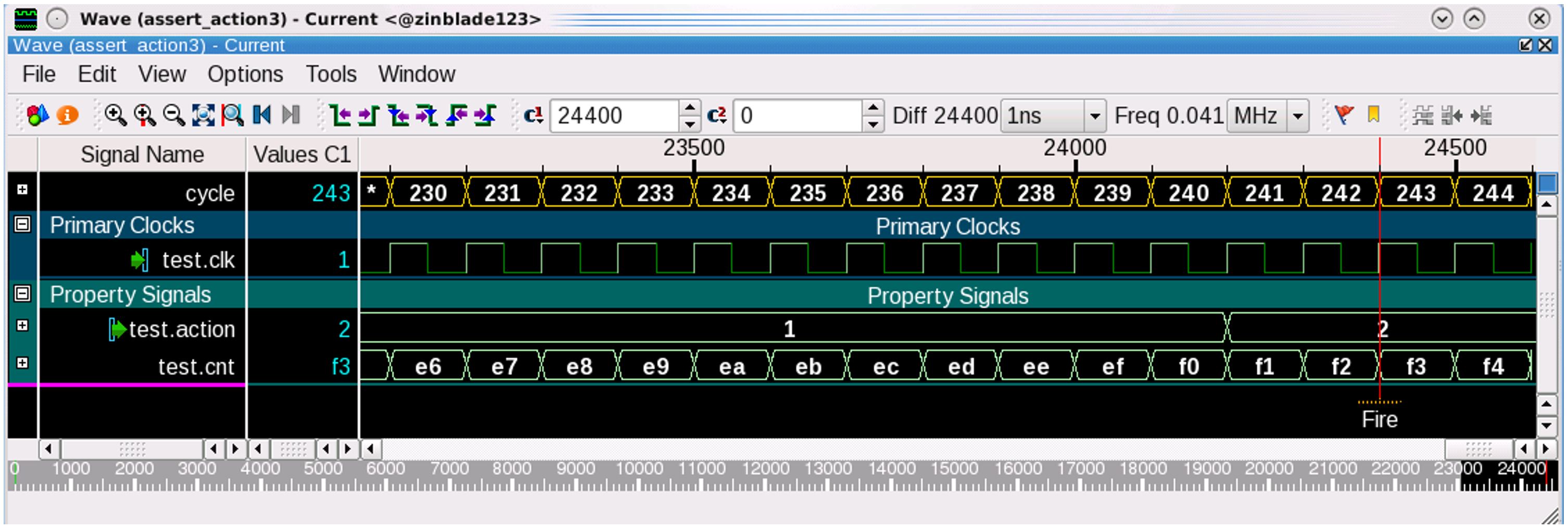
If we remove “do abs_cnt.do” from “Makefile” and rerun the test by using original “cnt” defined in the RTL, we will get error trace similar to the following one. We can see the firing happened at cycle 242 that is much longer than the one using abstract version of “cnt”. In real big designs, it may be impossible to formal to converge for big counters without abstraction.
Note that this strategy should mainly be used for bug-hunting – a full proof from this approach is not going to be valid if the rest of design relies on a particular number of cycles in between counter values. Again, as noted above, any CEX’s must be carefully reviewed to confirm the firing is being caused by design bug and not an overly-abstracted counter model.
Now that all your counters have been tamed, the next beasts to deal with are all the memories. We will show you how in Part 5 …
Until then, may your state spaces be shallow, and your analyses be exhaustive!
Jin Hou and Joe Hupcey III
for The Questa Formal Team
Reference Links:
Part 1: Finding Where Formal Got Stuck and Some Initial Corrective Steps to Take
Part 2: Reducing the Complexity of Your Assumptions
Part 3: Assertion Decomposition
Verification Academy: Handling Inconclusive Assertions in Formal Verification






Comments