How to Reduce the Complexity of Formal Analysis – Part 3 – Assertion Decomposition
In Part 2 of this series, we showed how reducing the complexity of you assumptions (a/k/a constraints) can really help the formal algorithms optimize the analysis setup, and subsequently reach solutions faster. In this post we focus on the significant benefits of simplifying assertion properties. Here is the challenge: it can be really tempting to encode the desired behavior of the DUT in exquisite detail with long, sophisticated assertions; because, let’s face it, the DUT *is* very sophisticated. But the reality for formal analysis is very counterintuitive at first: the truth is that assertions should be as simple as possible, with a sequential depth as short as possible, for best results. The trick is to “decompose” the complex behaviors you need to verify into their most basic elements, and trust that under-the-hood the formal algorithms will internally arrange them to take advantage of state-space symmetries and other clever optimizations that aren’t obvious to the naked eye. Let’s start with this simple example:
Suppose you had an error indication signal — “error” – that is assigned by the code “assign error = err1 | err2;” where “err1” and “err2” are used to detect two different error situations. The original assertion below verifies “error” that should always be ‘0’. When the Cone of Influence (COI) circuitry behind “err1” and “err2” are large, we can decompose the original assertion to verify “err1” and “err2” separately.

For complex assertions with product terms on the RHS, we can decompose them into a number of simpler assertions in the following way as shown in Figure 2 below:

Again, under-the-hood the formal algorithms will take the three simpler assertions and effectively verify these functions such that the combined properties infer the original one. This isolation of particular design functions makes the problem much more manageable for the formal algorithms, giving you a solution faster and with a minimum of compute resource.
Make sense?
Let’s step up to a larger example:
One way to decompose a big, end-to-end assertion property is based on a modular partitioning as shown below. Specifically, the end-to-end property (sketched at the top of Figure 3) is decomposed to verify each sub-module separately: P1 to verify Sub1, P2 to verify Sub2, and P3 to verify Sub3 (bottom of Figure 3). The results from this will be the same as if we ran on the big end-to-end property thanks to the “assume-guarantee” principle for this kind of decomposition, where we use proven properties as assumptions for proving downstream properties.
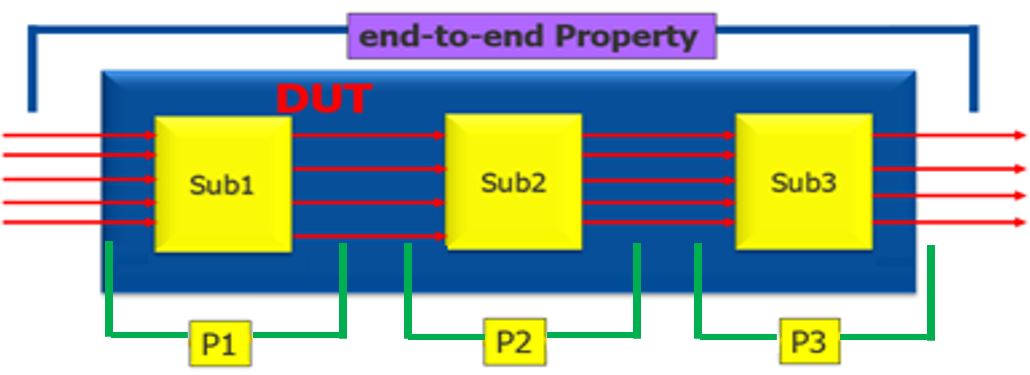
In this case, when property P1 is proven, it can be used as assumption for verifying P2 so that the design logic of Sub1 can be removed for verifying P2. When P2 is proven, it can be used as assumption for verifying P3 and the design logic of Sub1 and Sub2 can be removed for verifying P3. In this manner, COIs for verifying the individual P1, P2, and P3 assertion is reduced dramatically, giving the formal algorithms more room to breathe, and thus a much higher chance to prove all three of these simpler properties vs. trying to swallow a huge state space corresponding to the original end-to-end property and mass of logic.
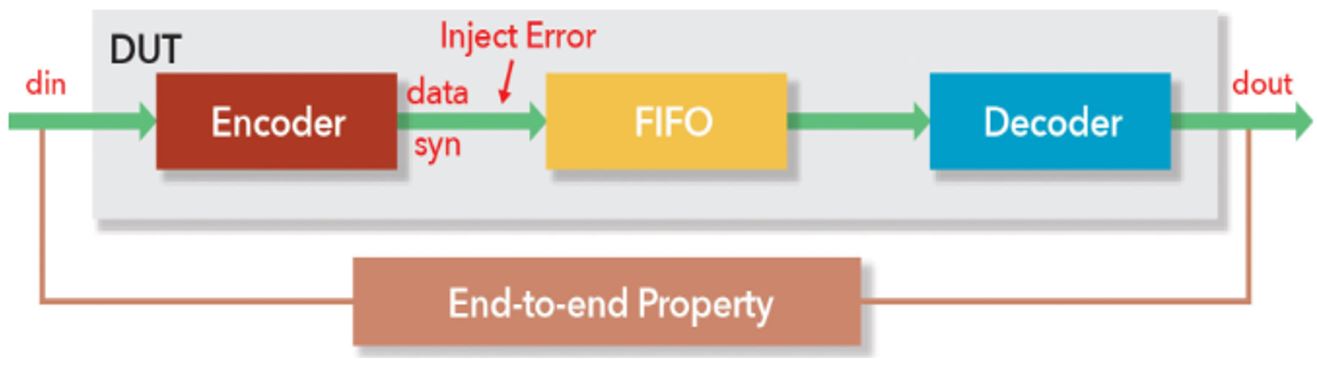
Another way to decompose an end-to-end property is to separate design functions such that the complexity is more manageable. Consider a basic Error Correcting Code (ECC) design below in Figure 4, where Encoder’s output “data” (combined ‘din’ and generated ‘syndrome’) is written into an FIFO, and then Decoder reads the FIFO and decodes “data”. The end-to-end property verifies that data can be corrected when errors are less than 3 bits. However, often an assertion like this won’t converge due to the complicated mathematical operations in the encoder and decoder, and the long latency and large state bits introduced by the FIFO.
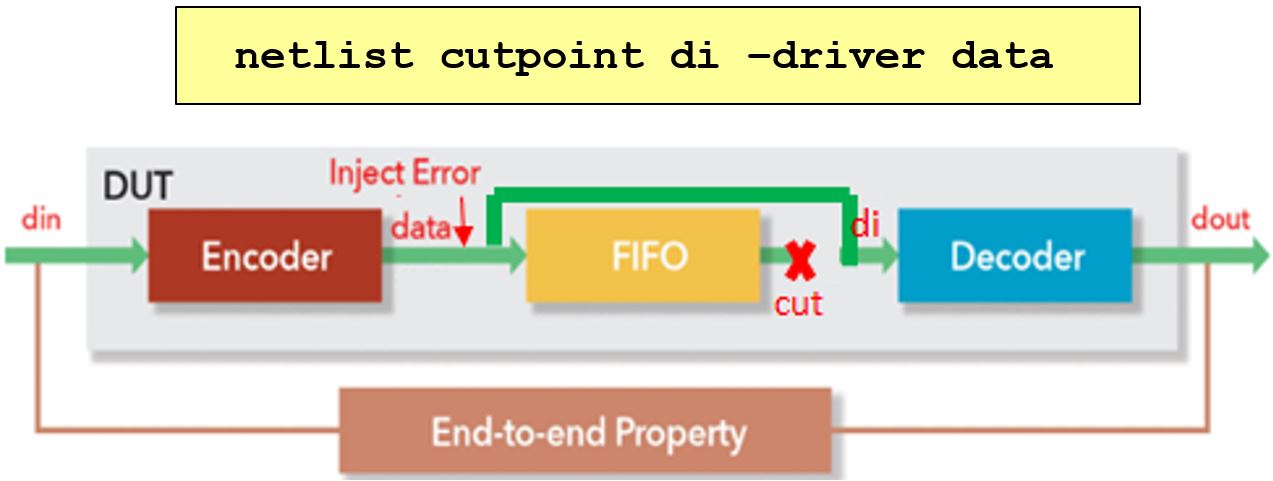
To verify this design, we can verify the Encoder and Decoder separately from verifying the FIFO. To do this, we can “cut” the connection from FIFO output to Decoder input, and then drive the Decoder input by Encoder output as shown in Figure 5 below. This can be non-destructively implemented by a simple tool command “netlist cutpoint”, which removes the FIFO from the Encoder and Decoder logic, and only considers the mathematical operations of ECC logic, taking out a lot of circuit complexity.
Next, inject 2-bit errors into the data path between Encoder and Decoder using the following code:
If the design works, “dout” should be equal to “din” – the assertion code to capture this intent is:
To verify the FIFO, we use the original design, but “cut” the output data and ‘syn’ signals to get rid of Encoder logic to reduce complexity (Figure 6). All other logic associated to FIFO is preserved.
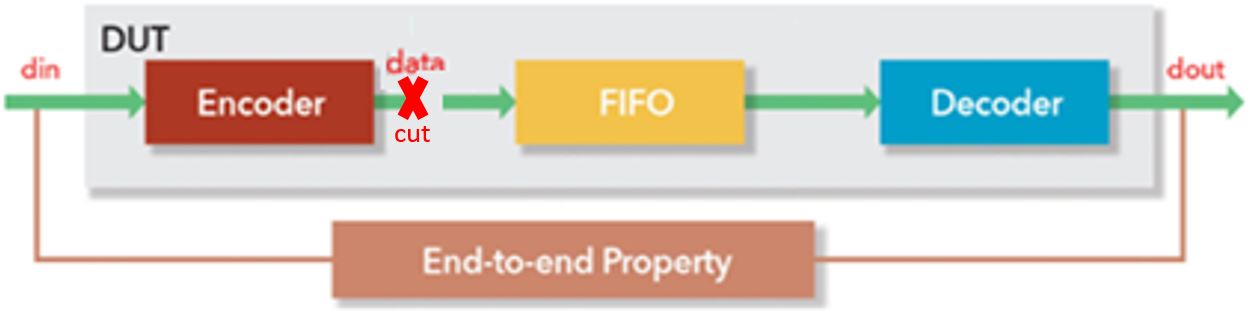
Now the ‘data’ becomes free inputs to the FIFO for the formal analysis. If the tool can verify that for any values written to FIFO, the values are read out in the correct order from FIFO, the data integrity feature of FIFO is proven, and the proof is still valid when data is driven by Encoder output in which case the data is a subset of free input. Using the Questa® QFL FIFO library, the tool can verify FIFO data integrity, no overflow, no underflow, and no timeout automatically.
What if you have tried all the above, but you are still getting a lot of “Inconclusives”? In successive posts we will show how to slay two big dragons that often cause big trouble: big counters and memories.
Until then, may your state spaces be shallow, and your analyses be exhaustive!
Jin Hou and Joe Hupcey III,
for The Questa Formal Team
Reference Links:
Part 1: Finding Where Formal Got Stuck and Some Initial Corrective Steps to Take
Part 2: Reducing the Complexity of Your Assumptions
Verification Academy: Handling Inconclusive Assertions in Formal Verification





Comments