D-Cubed 2D Components release highlights
D-Cubed 2D components are integrated by software developers to add functionality to the sketching environment of CAD/CAM/CAE and AEC software applications. These applications are used to design, analyze, visualize, and manufacture products from consumer goods to aircraft engines and commercial buildings.
D-Cubed 2D DCM version 73.0
D-Cubed 2D DCM (2D Dimensional Constraint Manager) is widely acknowledged as the leading 2D geometric constraint solver. In addition to driving the sketcher in many CAD products, 2D DCM is used in CAM, CAE and other geometry-based applications. Enhancements introduced in version 73.0 of D-Cubed 2D DCM are described below.
Improved support for conic curves
In 2D DCM conics are defined by three control points and a shape parameter which defines whether the curve is an ellipse, parabola or hyperbola. For certain control point conditions and rho value combinations the conic curve defined is degenerate. For example, a portion of an ellipse with zero minor radius and non-zero major radius. Version 73 introduces an option for applications to request that solutions that will result in a conic curve that is degenerate are rejected by 2D DCM.
Improvements to over-defined status codes
2D DCM informs an application about the status of dimensions and constraints such as well-defined, over-defined and under-defined. 2D DCM now correctly identifies more constraints as over-defined which were previously incorrectly identified as solved. This change will assist applications and users to understand and fix over-defined models.
Half-space defined between offset curves
2D DCM use the half-space property of a distance dimension to define the sign of the distance, so that positive values will solve on one side and negative values on the other side of a line, for example. In this version of 2D DCM support for half-space solving has been extending to include the offset distances between a base curve and its offset.
Model satisfied – fast option
The model satisfied functionality informs an application whether the dimensions and constraints have been solved. As an optimisation an option is now available to request that 2D DCM will return immediately on finding an unsatisfied constraint, instead of checking the entire model.
Technical preview – enhanced support for inequalities
2D DCM has for a long time provided an interface to define inequalities on variables to specify a minimum and a maximum value, for example:
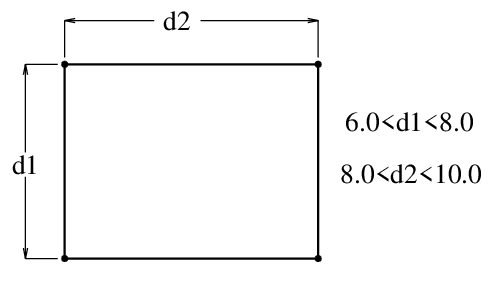
Support for inequalities is more complex than for normal dimensions, with resultant limitations on reliability and performance. A new more stable and reliable algorithm was recently introduced in 3D DCM, and a similarly improved algorithm is now available in 2D DCM in a trial form. In subsequent releases the new 2D DCM algorithm is expected to replace the old algorithm.
D-Cubed PGM version 73.0
D-Cubed PGM (Profile Geometry Manager) enhances the productivity of sketchers. It does this by working with higher level geometric data and not individual curves. Examples include offsetting loops while inserting, extending and trimming edges, adding constraints to loops rather than to individual curves, and solving the shape of loops while maintaining their perimeter length or area. PGM is often used to add capabilities to a 2D DCM-based sketcher. Key enhancements introduced in version 73.0 of D-Cubed PGM (Profile Geometry Manager) are described below.
Model satisfied improvements
The model satisfied functionality informs an application whether the dimensions and constraints have been solved. 2D DCM will now check PGM constraints, including offset relationships and length and area.
PGM satisfied functions have also been added to enquire whether a PGM loop and offset constraint are satisfied. Improved discontinuity reporting on splines.
Improved discontinuity reporting on splines
PGM will now identify and classify discontinuities on spline edges based on the control point positions. A curve with adjacent coincident control points at different knot values will have a region parameterisation with zero physical length.


