How to Reduce the Complexity of Formal Analysis – Part 6 – Leveraging Data Independence and Non-Determinism
If you know the dependencies – or lack thereof – in your design, you can exploit two very fundamental characteristics of formal analysis that will really simplify things for the formal algorithms; giving you significantly better wall clock run time and memory usage performance: Data Independence and Non-Determinism. Along with a little design knowledge and some forethought, leveraging either of these can cut down your formal analysis to a matter of minutes vs. days. Let’s start with some definitions:
Data Independence (DI): your property/assertion does NOT depend on the specific values of the data.
Non-Determinism (ND): this is a technique that uses “free variables” implemented as un-driven wires or extra inputs in a checker to tell the formal engines they are free to consider any cases involving all possible values of the variables at once.
Taking advantage of Data Independence is as simple as reducing the width of a data path in a property, as long as the property/assertion does NOT depend on the specific values of the data. For example, for verifying the data integrity of a FIFO, you only need to check that data written in will be read out correctly and in the right order — whether the FIFO width is 32 bits, 8 bits, or just 1 bit. A property that captures this intent is effectively data independent! Consequently, you can go ahead and reduce the width of the FIFO to 1 bit in the property code and the result of the formal analysis will still be valid.
Non-Determinism is about another form of freedom – the freedom not to care what a given input signal’s value is a-priori. Consider the following: if the variable “latency” is really big, this assertion can introduce a lot of extra cycles into the analysis.
Fortunately, we can recode it as follows where “cnt” has (log2 latency) bits that reduces the number of states. We only check the latency between one “req” and one “ack”, while introducing a new free variable, “start”, to let formal consider all random start times for “req”, thus consider all “req”
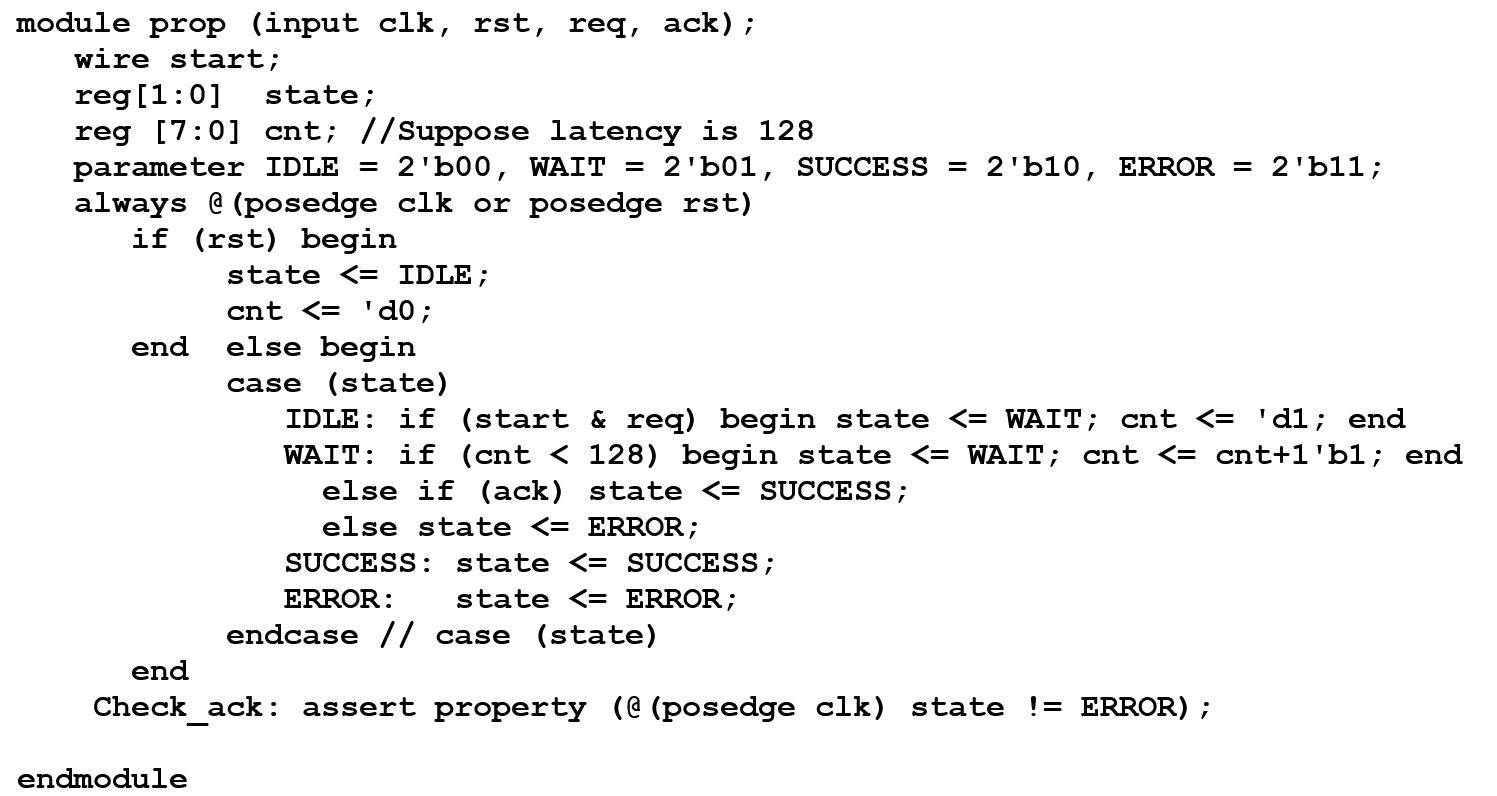
Still unclear? The state diagram below corresponds to the ND-exploiting “start” free variable:
As you can see, the addition of the “start” signal limits the check to only one pair of “req” and “ack”. However due to the non-deterministic feature of the free “start”, formal considers all possibles, and the result is valid for both proof and firing.
Recall that assertions are essentially synthesized to logic. Hence, when the latency is 128, the logic introduced by the original assertion “Check_ack” has 128 flops that are a pipeline to remember the value of “req”, In contrast, the logic introduced by the assertion using the ND technique only has 10 flops (2 for “state” and 8 for “cnt”). Clearly, the ND version’s dramatically lower flop count means the complexity for formal analysis is significantly reduced, which will directly translate to faster run times and lower memory usage.
Once you get the hang of applying DI and ND, before you know it you will start to see opportunities to apply these principals everywhere. Your colleagues will marvel at your formal analysis expertise as you get more and more proofs or CEXs, fast.
We trust that the various techniques to resolve Inconclusives that we have reviewed in this six part series will make your more productive. Please let us know in the Comments below, or offline via email!
May your state spaces be shallow, and your analyses be conclusive!
Jin Hou, Joe Hupcey III
for the Questa Formal Team
Reference Links:
Part 1: Finding Where Formal Got Stuck and Some Initial Corrective Steps to Take
Part 2: Reducing the Complexity of Your Assumptions
Part 3: Assertion Decomposition
Verification Academy: Handling Inconclusive Assertions in Formal Verification



Comments