Demystifying Electromagnetics, Part 2 – Wires
I Dream of Wires
Just as a pipe is a conduit for fluid flow, so a wire is the same for the flow of electric charge. Both flows are considered ‘currents’. Coming in many sizes, but all of similar shape and commonly made of Copper, they allow for the movement of electrons (charge) through them, when forced to do so.

Where does this force come from and what’s so special about Copper anyway? To answer that, let’s carry on from Part 1 and look a bit more into the Electric Field.
From +ve to -ve
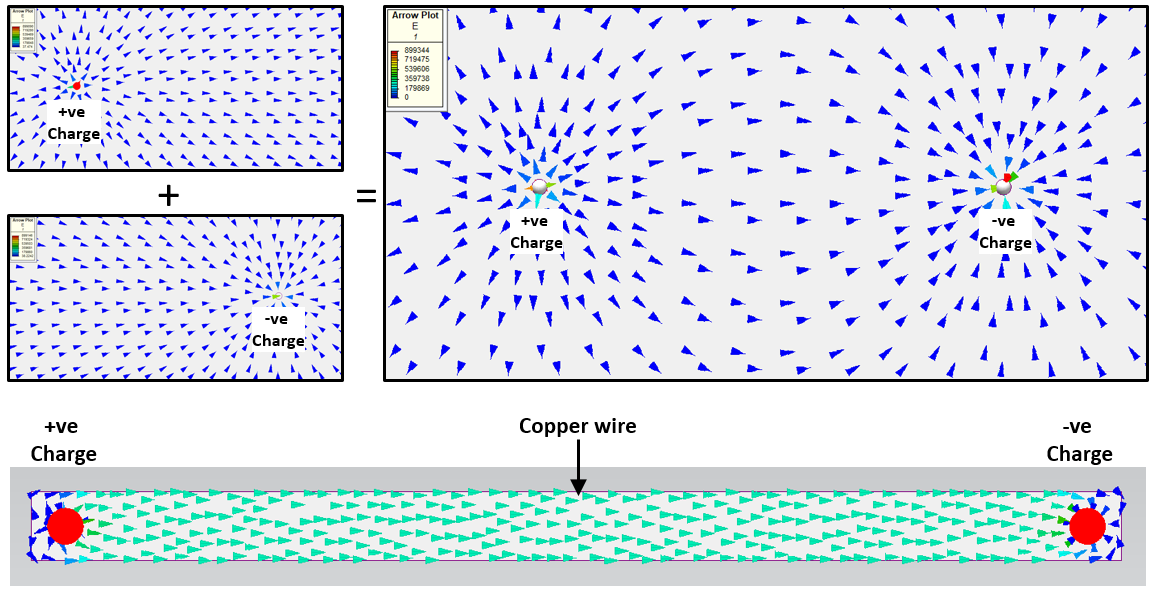
The electric force field that a charge generates acts in a certain direction. The common notation is that if the charge is +ve (positive) then the force vectors point away from the charge, opposite for when the charge is –ve (negative). So generally the vectors indicate the direction the force would be applied on another +ve charge, were it to be placed in the field.
What happens if you have a +ve charge point (a deficit of electrons) near a -ve charge point (an excess of electrons)? The 2 force fields combine into a single force field. This combining is known as superposition, electric (and magnetic, potential fluid flow, thermal conduction) fields exhibit superposition behaviour:
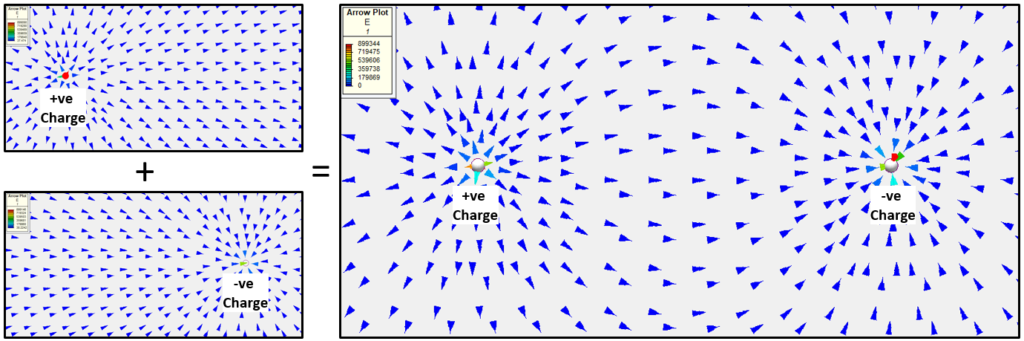
Remember the arrows show the direction that the force would be applied to a +ve charge when placed somewhere in that field. The magnitude of this force can be calculated using F=Eq, where E is the field strength (in units V/m or N/C) and q is the charge (measured in Coulombs, C). So if a free +ve charge were placed in that field it would ‘gravitate’ to the –ve charge point (you’ve heard of mixed metaphors, well how’s that for a mixed analogy!).
When Charges Start to Flow
In the above example both point charges sit in vacuum (or air, as air has the same permittivity as vacuum) and the electric field is just one of potential, nothing is actually flowing through it.
In air though, if the electric field strength is REALLY big (~>3 kV/mm) it’s strong enough to free up the electrons in the air (ionization) whereupon they start to flow. This is how lightning works. The field strength (Newtons per Coulomb) rips the electrons from the atoms in the air to the extent where it stops being a dielectric and turns into a conductor. A gas, such as Neon under low pressure, ionises at much lower electric field strengths, and that’s how fluorescent lights work. The photons that are produced in both cases are emitted due to side effects of this ripping of the electrons from their happy atomic orbits.

What’s so Special About Copper?
A dielectric material is one through which an electric field can permeate, but the charges do not flow. Primarily because all the electrons are happily spinning around, and bound to, their nuclei. A conductor on the other hand is one where there are ‘free’ electrons that would readily flow, were an electric field to act on them.
Let’s go back to our 2 charge example and connect them with a copper wire. Think of the +ve and -ve charges as the two terminals of a battery.

The Copper not only gathers the electric field and channels it through itself, it then allows its charges to flow. Unlike the point charges floating in air, where the field strength dropped off based on 1/r2, a conductor (with a homogenous material and constant cross section) maintains the same field strength E (V/m) throughout its length.
Wait, what, a constant E field, how does that work? Let’s use analogy again. If you fixed the ends of a metal bar at different temperatures, you get heat flowing down that bar in 1 direction. So long as the bar is all made of the same material and has a constant cross section, the temperature gradient down that bar will be constant, i.e. a constant degC/m. The point being that the bar channels that heat flow down itself so long as its thermal conductivity is much higher than the effective thermal conductivity of its surroundings. Similar for the Copper wire, compared to the electrical permittivity of the surrounding air (or any other dielectric), its effective permittivity is very large, channels the electric field (the ‘permeating charge’) through itself at a constant V/m, i.e. constant E field*
(*an overly simplified explanation that doesn’t go nearly deep enough into the physics, but one that I hope will convey the nature of a fixed E field in a conducting wire).
Not another mystery?
Mystery #3 – The electrons are flowing in the opposite direction to the electric force field vectors
Maybe more just confusion due to ‘unfortunate’ notation than an actual mystery. A +ve charge is a deficit of electrons. This attracts a –ve charge (an excess of electrons). So the electrons themselves will be attracted to, and will flow towards, the +ve charge point (right to left in the above image). The electric force field notation however is to show the force field vectors moving away from the +ve source charge point. To reconcile this you can think of the deficit of electrons flowing from +ve to –ve are like holes of missing electrons that themselves flow.
Again, What’s So Special About Copper?
Answer: it doesn’t require much electric field force to get its electrons moving. It’s a very good conductor. There’s a single electron in the outer shell of a Copper atom that isn’t so strongly bound to its nucleus, its a ‘free electron’. Give it a slight push and it detaches from its atom and goes with the electric force field generated flow. It has nuclear family commitment issues. The only other metal that is a better conductor is Silver, just a shame there’s not much of that at our disposal and what there is is often wrapped around our fingers or draped around our necks.
Electric Current is a Flow Rate
As mechanical engineers we’re used to the concept of mass flow rate (kg/s) or heat flow rate (W or J/s). Electric current is simply a charge flow rate, Coulombs per second (C/s) defined as Amps (A) and noted as I. A Coulomb remember is -6.24151×1018 electrons. So 1A is that many electrons moving through a cross section of a conducting wire every second.
Consider a free electron in a Copper wire. The force it experiences = Eq (analogous to F=ma)
The subsequent acceleration the electron with mass me experiences = Force/Mass = Eq/me
The velocity of the electron at time t after it starts moving = time x acceleration = tEq/me
Take a portion of wire with the constant Electric force field inside it, let loose a free electron, off it goes (OK, OK, as discussed above, consider the blue dot an electron hole):
Do they keep on accelerating for ever?
No. They quickly hit a Copper atom. When they do so, a new free electron is dislodged which then accelerates off until it too hits a Copper atom.
Drift Velocity
The time it takes for an electron to collide with an atom is called the ‘relaxation time’ denoted by τ
So the maximum velocity when an electron hits an atom = τEq/me
The average velocity (from 0 to max) of the electron is therefore half of its maximum velocity. This is called the drift velocity = τEq/2me
The electric field E can be considered as Voltage drop over a distance L. So the drift velocity can be written as τqV/2meL
In reality there are countless free electrons, all smashing into Copper atoms at various times. It’s like a cloud of free electrons that drift through the Copper, thus the name.
Ohms Law is just Electric Charge Flow Rate
For fluids, a mass flow rate is measured in kg/s and can be calculated from the fluid density x velocity x cross sectional area that the fluid flows through.
Electric current flow is analogous but in terms of charge flowing through an area per second, C/s, and can be calculated from the charge density x drift velocity x cross section area.
- The charge density is just the number of free electrons per volume x the charge of an electron, Nq. The former is a property of Copper, the latter is an inherent property of electrons.
- We know the average velocity of the electrons, the drift velocity, τqV/2meL
- The cross sectional area is that of the wire through which the electrons flow, A
Putting it all together yields the following calculation for the current I in a wire of cross sectional area A and length L, i.e. Ohm’s Law:
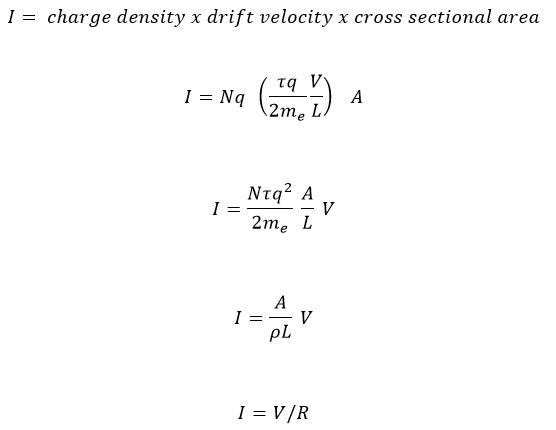
Where R is the electrical Resistance (Ω):
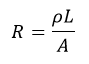
And ρ is the electrical resistivity (Ωm), a property of the material:
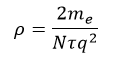
Joule Heating by Accident
Electronics thermal management is all to do with the efficient removal of heat from where it is generated. This source of heat energy always comes down to some electrical conductor (semi or otherwise) where the power dissipation is termed Joule heating and is generally considered as VI, Voltage x Current.
As we’ve just covered, current is defined as flowing Coulombs per second (C/s). Voltage is the potential energy of a charge (J/C). Multiply to 2 together and you get J/s -> W.
But where does this energy really come from? Yet again, it comes down to mechanics, rather dynamics. Each time a free electron, accelerated by an electric field, crashes into a Copper atom, its momentum is transferred to that atom. That atom’s kinetic energy increases as a consequence. It wobbles more, and it wobbles really quickly:
It’s like throwing a cricket ball really hard at a bell in a clocktower, the bell will start to vibrate and ring (no, I’ve never done that either, but never say never!).
A typical speed of the wobble of a Copper atom is 1500 km/s, whilst a typical drift velocity is 20 μm/s. And sure, the above animation is somewhat simplistic in that the atoms are always wobbling if they have a temperature > 0K, the electrons colliding with them only increase that wobble. The more they wobble (the hotter they are), the time it takes for an electron to hit an atom (τ) reduces, electrical resistivity goes up thus the electrical resistance increases with temperature.
Temperature is just a measure of the kinetic energy of the atomic wobble and is caused by the momentum of the free electrons being transferred to the atoms when they collide. From that a whole industry has emerged to channel that kinetic energy way through heat spreaders, heatsinks, moving air, coldplates, heatpipes etc. Such is the reason for electronics thermal management.
Anecjoke
As is tradition, let’s end with an anecdote or joke. O dear, this is a dreadful one, my apologies:
Why did Mr Ohm marry Mrs Ohm?
He couldn’t resistor