Demystifying Electromagnetics, Part 1 – Fields and Analogies
Who Are You?
If, like me, you’re a Mechanical Engineer with a thermo-fluids background then Electromagnetics might appear both mysterious and impenetrable. We’re used to continuums where things flow, tangible things like fluids and heat, things we can see or feel. Electromagnetics (EM) deals with invisible force fields that as humans we can’t readily sense. Sure, at school we were taught about magnets attracting or repelling, magnetic fields around wires, something to do with fingers of your right hand (or was it the left hand?) but that was (many) years ago.
EM plays a key role in the technology of the modern world and, as engineers, it’s worth having at least a working knowledge of electric and magnetic fields, EM machines and devices. This blog series will strive to demystify (low frequency) EM by way of pictures and analogies, with as few equations as possible, by introducing a series of applications of increasing complexity. From wires and transformers through to particle accelerators, electric motors and Maglev trains, join me on what I hope will be an exciting voyage of discovery and understanding!
In this first blog we’ll and start to look into the electric field with the use of some analogies. But first, some basics…
Charge
Electric and magnetic fields only act on electric charges, that’s it, simple as that. As far as demystification goes, we’re off to a good start.
So, what is a charge? Well, it can be negative or positive. Electrons have a negative charge and protons have a positive charge. If you have something with the same number of electrons and protons then it is neutral, i.e. it has a charge of zero.
Personally I like to think of charge as either an excess or deficit of electrons. By definition, if you have 6.24151×1018 extra electrons then you have -1 Coulomb (C) of charge. If you have a deficit of 6.24151×1018 electrons then you have a charge or +1 Coulomb (C). And yes, this opposite notation does get a bit confusing later on when dealing with a flow of charges (i.e. a current).
Is Gravity Mysterious?
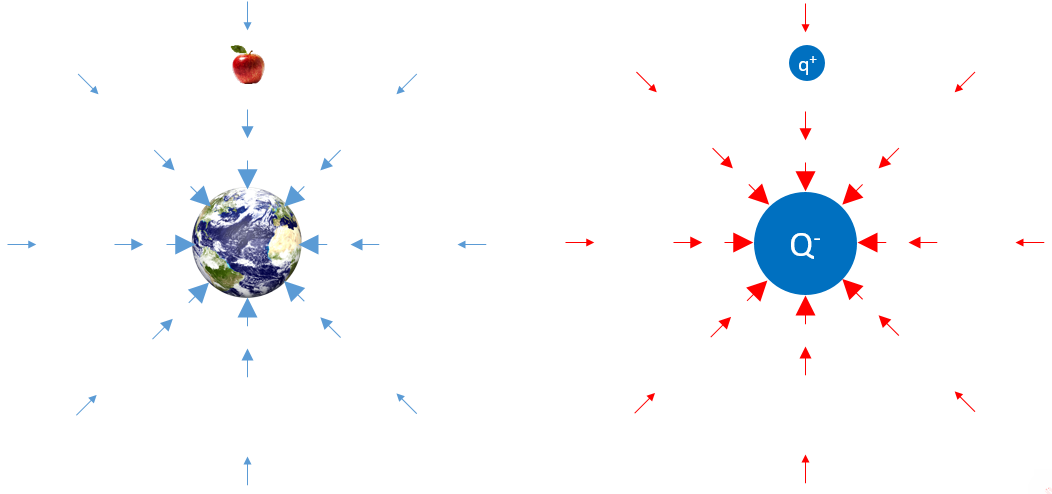
We should be quite familiar with gravity. It stops us floating off into space for a start. What creates gravity though? More precisely, what creates a gravitational field? Answer: Mass. Any mass creates a gravitational field around it.
Mystery #1 – this field exists even in a vacuum.
What? Doesn’t it need some kind of medium to ‘carry’ it, to ‘propagate’ it? Nope. I’ve found the best way to comprehend this is just not to question it. How’s that for a cop out.
Is an Electric Field Mysterious?
It’s only as mysterious as a gravitational field due to how similar it is. What creates an electric field? Answer: Charge. Any non-zero charge creates an electric field around it:
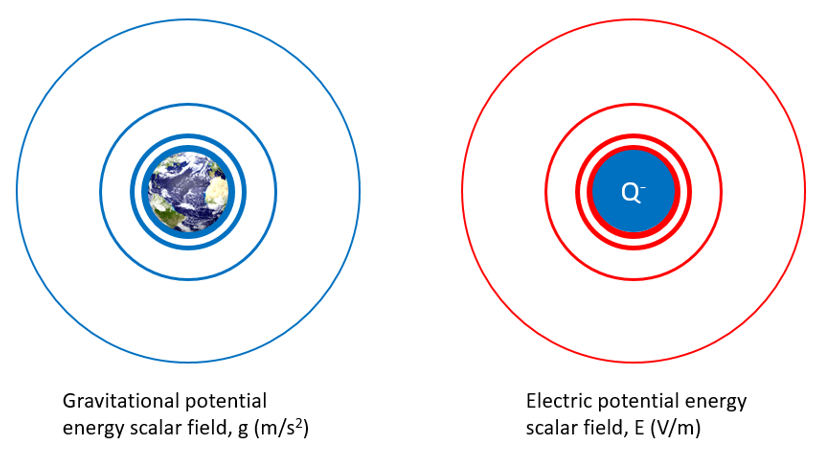
Both gravitational and electric fields can be considered as fields of potential energy. Closer to the source of the field, the stronger the field is. On the surface of the earth the strength of the gravitation field is 9.81 m/s2. That strength drops off proportional to the distance away (r) by 1/r2. Go twice as far away, the strength decreases by a factor of 4.
An electric field behaves in exactly the same way, propagates/permeates even through a vacuum, drops off in strength proportional to 1/r2. It has different units though, V/m. Another way to think about it is that the charge creates a Voltage field around it, the gradient of which is called the Electric Field, E.
Force Fields
It’s often easier to think of the field not as a volume of differing potential energy, but as a force field. The stuff of Sci-Fi.
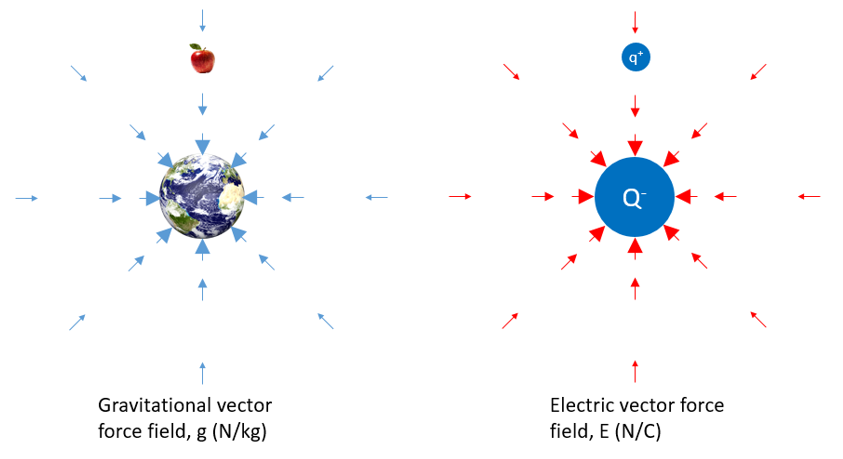
Still the same fields, just with rearranged units being a force per unit of the thing creating the field. The arrows indicate the direction a force would be applied on something if it was put into the field. That something being either a mass that the gravity would act on, or a charge that the electric field would act on.
The terms would and if are important. The potential energy field is potential only in that it just sits there until it has something that it could potentially act on. The apple in the tree at Woolsthorpe Manor in the UK in the summer of 1666 had potential energy which converted into kinetic energy as it fell onto Isaac Newton’s head.
It’s all Just F=ma
g, the strength of the gravitational field, is called ‘acceleration due to gravity’ for good reason. As F=ma, then a=F/m. So the gravitational field is simply the force that would be applied on a mass in that field. Units = N/kg. Or in terms of the force, F = mg.
The electric field (E) is just the same. The electric field is the force that would be applied on a charge in that field. Units = N/C. Or in terms of the force, F = qE.
Strictly speaking the above holds true for when the thing being acted on is so small, that its own field can be ignored
An Important Distinction
A gravitational field is similar to an electric field in all but two ways. A mass will always attract a mass, the direction of the gravitational force vector is always such that the 2 masses are pulled together. A charge will only attract a charge of the opposite sign. If they have the same sign then the force will repel the charges away from each other. If there was such a thing as negative mass, we’d at least have flying cars by now. Same signed masses attract, same signed electric charges repel and you never have different signed masses.
Vectors, so is Something Flowing?
Analogy has proved useful so far. But can we go so far as to say ‘hey, we’ve got vectors, that’s just like heat flow’? (as a thermal engineer with a focus on electronics cooling, I’m going for the heat flow analogy instead of the alternative fluid flow analogy)
We can go as far as we like, so long as the analogy holds and demonstrates some value, some utility.
Heat Conduction
As promised, so far I’ve steered clear of any equations. However, with my apologies, I need to get a little mathsy now.
Consider a heat source, Q(W), embedded within a solid material that has a thermal conductivity k (W/mK):
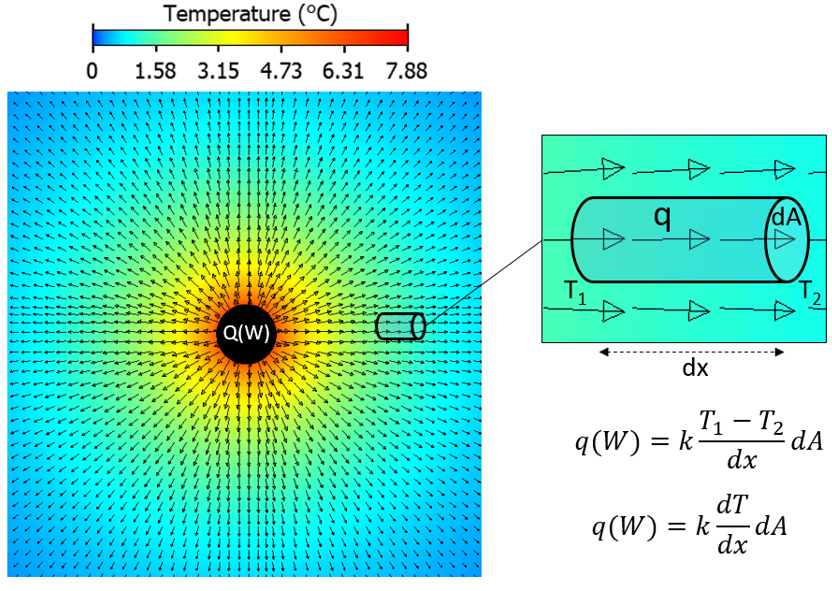
The heat flows out from the source, through the material, ultimately dumping into a fixed temperature remote ambient. The material is hottest close to the source. Consider a small volume in that heat flow field (a control volume, mesh cell). The amount of heat (W) that flows through that volume (in a single direction) is calculated based on Coefficient x Gradient x Area. The coefficient is the thermal conductivity, the gradient is the temperature gradient and the area is just really small.
As equations go, at least it’s quite a simple one that Fourier figured out in the early 1800s.
Electric Permittivity
Let’s take the same approach for an electric field. A charge, Q(C), is placed in a vacuum that has a ‘permittivity’ represented by ε0 (8.85418×10-12 Farad/m). This permittivity is analogous to thermal conductivity, main difference being that thermal conductivity is zero in a vacuum.
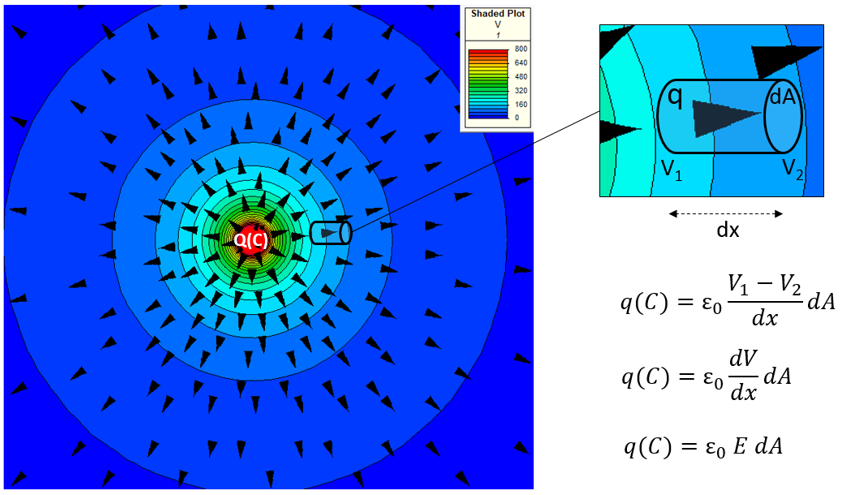
It looks as if the charge, Q(C), is ‘flowing’ out from the source (but remember these are just force field vectors). Looking at the coefficient x gradient (E) x area calculation, the units of the quantity going through that control volume are indeed Coulombs. However:
Mystery #2 – THE CHARGE IS NOT FLOWING
Electrons (excess or deficit) are NOT physically moving out from the source through the vacuum. However the electric field is generated as if the charge ‘permeates’ the space around it. Alternatively you might say that the charge ‘influences’ the space around it, as if spreading outwards setting up the electric field as it went. The further away from the source charge, the less influence it can exert, the weaker the electric field. ‘Influencing across a distance’. In lieu of a better word, and considering I don’t think we have a word to describe it exactly, I’m going to stick with ‘permeate’ (as this term will pop up again when describing magnetic fields).
Conservation – What Goes In Must Come Out
Even though nothing is physically flowing through the electric field, the charge is just influencing/permeating its surroundings, let’s continue with our continuum mechanical engineering thinking and look at conservation.
‘Energy can neither be created nor destroyed’ underpins most, if not all, of physics. What goes in must come out, there must be a balance. From a thermal engineering perspective we’re used to considering this in terms of thermal energy. If you considered a closed surface, of any shape, then the number of Watts flowing out of that surface must = number of Watts flowing in + any source of Watts dissipated inside the volume that the surface bounds.
Even though in one case heat is flowing, and in the other case the charge permeates the electric field, conservation is demonstrated in both:
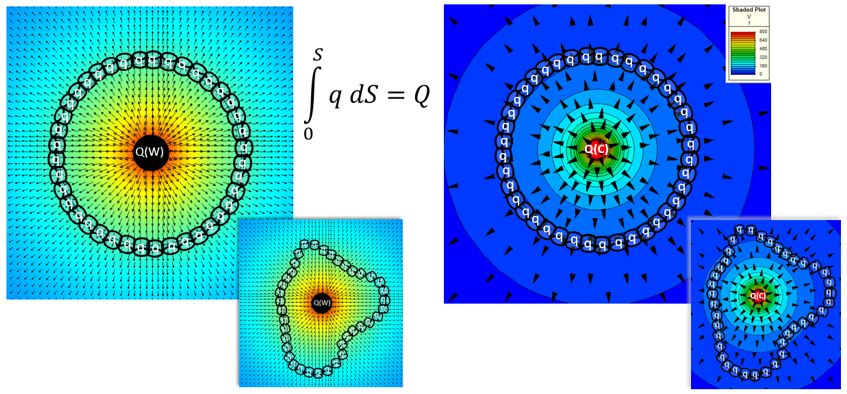
Add up all the stuff flowing/permeating through that closed envelope (S) and you get what was being added inside that envelope. Be it Watts or (non-flowing) Coulombs, regardless of the shape of that envelope.
Thermally this is just conservation of heat. From an EM perspective this is the first of Maxwell’s 4 governing equations (Gauss’ electrostatic law). Not bad going considering we’re only on the first blog in the series!
Coefficient x Gradient x Area
I hope you agree that analogy has proved a useful tool when introducing the Electric Field. It certainly helped my understanding, linking it back to what I was already familiar with.
The analogies can be further broadened to cover Magnetic Fields, Mechanical stress/strain and of course convective fluid flow systems. All based on the concept of something ‘permeating’ (sometimes flowing), a gradient that drives it and some coefficient that determines how well the medium allows that quantity to ‘permeate’ it. Summarised in the following tables:
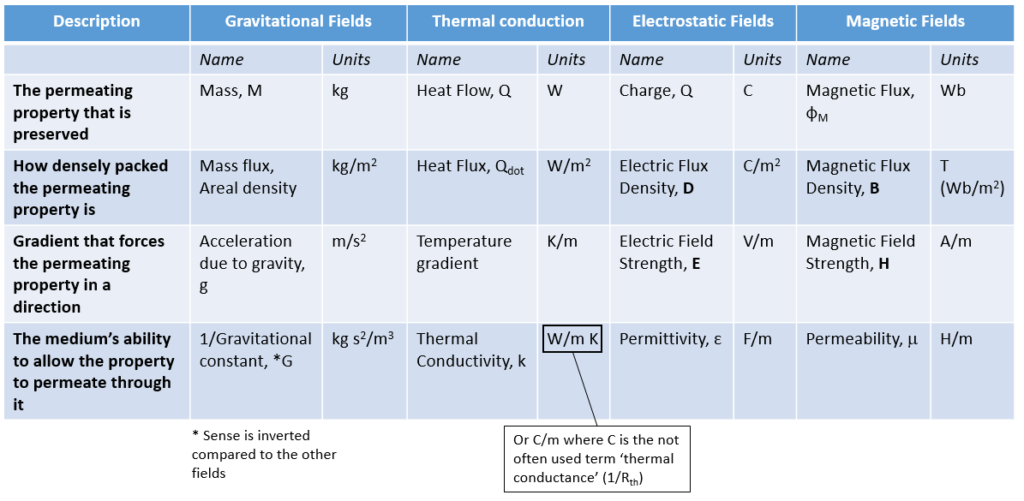
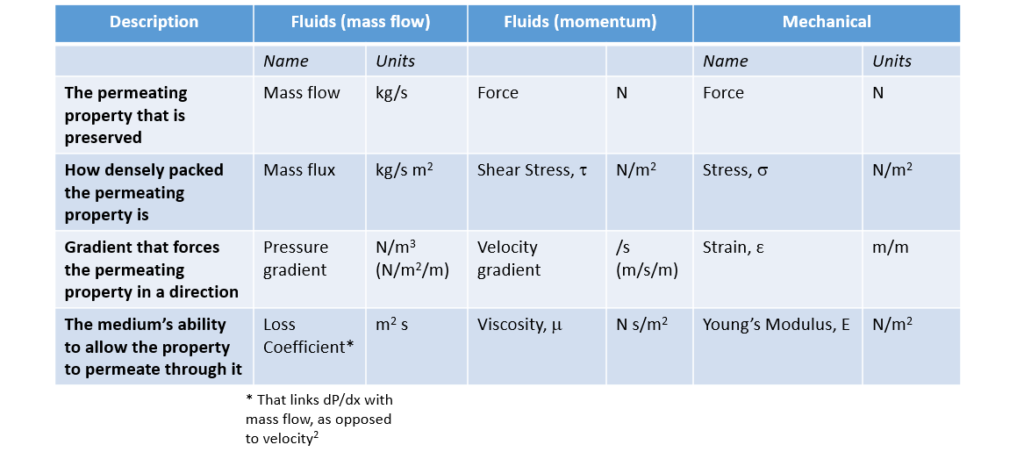
With convection of fluid mass, things get a little more complex in that the flow need not align with the direction of the pressure gradient, unlike all the other diffusive based ‘flows’.
Energy is Everything and Everywhere
One final comment on the above analogy tables… You can have fun with units, recasting them in various forms, all consistent, just using differing unit types. When recasting the ‘permeating’ properties in terms of Energy (J) you get the following:

(I took a liberty and used little v to represent velocity) Regardless of the ‘physics’, the analogous behaviour of these disparate fields is seen in the similarity of the energy based units of what is permeating, conducting, diffusing, convecting etc. They all somehow consistently deal with the storage and transmission of energy.
Anecjoke
By way of reward (or punishment) I’ll close off each blog in this series with either an anecdote or a joke, an anecjoke if you will. I hope you’re charged up enough to appreciate this one:
An electron and a positron walk into a bar.
Positron: “Your round.”
Electron: “Are you sure?”
Positron: “I’m positive.”