Chaotic Fluid Dynamics Part 2 – Butterflies

For want of a nail the shoe was lost.
For want of a shoe the horse was lost.
For want of a horse the rider was lost.
For want of a rider the message was lost.
For want of a message the battle was lost.
For want of a battle the kingdom was lost.
And all for the want of a horseshoe nail.
Sensitive dependence on initial conditions is by no means a new concept. Variations on the above proverb can be traced back to the 13th century. In the 1952 Ray Bradbury short story “A Sound of Thunder”, a time traveler from 2055 accidentally steps on a butterfly in a trip to the late Cretaceous period only to find that on his return some words are spelled and pronounced strangely, people behave a little differently and the recent loser in the US presidential election is now the winner (!). Wind forward to the 1998 rom-com “Sliding Doors”, where a story bifurcates into 2 timelines due to a missed train, and so the phrase ‘a sliding door moment’ became popularised.
Edward Lorenz
Edward Lorenz was a meteorologist at MIT and, in the winter of 1961, he made a discovery that would herald what is often called the 3rd scientific revolution of the 20th century – chaos theory (after relativity and quantum physics).

The discovery was due to a typo. Running a 12 equation weather prediction model on a Royal McBee LGP-30 computer, he decided to rerun a simulation and manually typed in the initial conditions for that run. Due to decimal place truncation on a printout, he entered 0.506 instead of 0.506127 which was used in the previous simulation. Off he went to get a cup of coffee. When he got back he found that the results he saw differed from the original run:
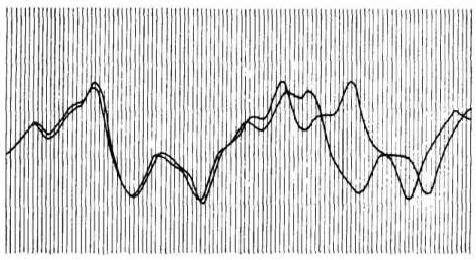
One might have expected that such a small difference in the initial condition, not even big enough to visible on the above print out of his 2 simulations, would quickly be damped out and that the 2 simulations would become indistinguishable. The opposite was true. The ramifications for weather forecasting were huge and it was the seed of chaos theory that spawned research in so many disciplines in the 70s, 80s and to this day.
It also spawned Jeff Goldblum’s chaos mathematician Ian Malcolm in Jurassic Park, mmm…

The Butterfly
Lorenz’s seminal 1963 publication ‘Deterministic Nonperiodic Flow’ went on to plot the evolution of a simplified desciption of Rayleigh–Bénard convection (a common analogue for atmospheric convection) not as single parameter vs. time graphs, but by plotting integral properties of the flow against each other in phase space for what has become known as the Lorenz Attractor:
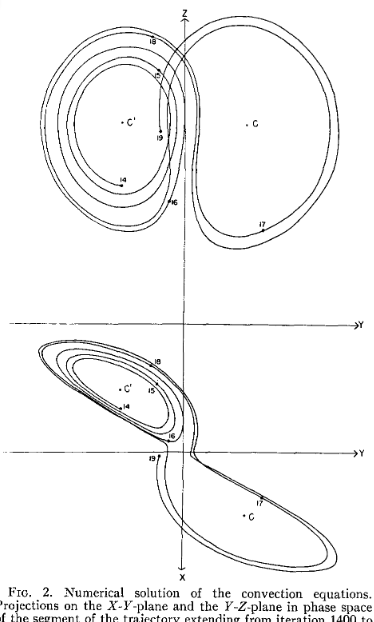
Although he original described such small perturbations of initial conditions as being like the flapping of a seagull’s wings, it was recommended by a colleague that he used butterflies instead. It was that that formed the title of a presentation to the 139th meeting of the American Association for the Advancement of Science in 1972 “Does the flap of a butterfly’s wings in Brazil set off a tornado in Texas?”
It is a poetic coincidence that the shape of the Lorenz Attractor looks so much like the shape of a butterfly’s wings.

Sensitivity Demonstrated by Simcenter FLOEFD
So, can Simcenter FLOEFD for NX be used to replicate this sensitive dependence on initial conditions? Let’s find out!
Using the same model as shown in Part 1, the following animation compares the evolution of the convective flow when the bottom wall is at 30 degC with when it is set to 30.0001 degC (a 0.001% difference in the bottom/top wall 10degC dT, as small as a butterfly compared to a tornado):
Up until about 20s, the 2 models are pretty much identical. Then small differences are seen which diverge over time until the predictions differ wildly. As good an example as any why weather prediction can be OK in the short term, but tends to be much less accurate beyond that.
Maybe ‘wildly’ is too strong a word, there is still upflow and downflow with oscillating convective cells that transport the heat from the bottom to the top in both models. Underpinning the turbulence there is a common coherent structure. Regardless of initial condition, both models are attracted to a somewhat common state. A so called ‘strange attractor’, but more on that in Part 3.