Shift gears for VOF simulation speed-up with Implicit Multistep 

As a child do you remember getting your first bicycle with gears? 

I do. I think everyone probably does. 

Our street was a little over 200m long. I just checked, in my memory, I am sure it was much longer! It had two other key characteristics. Firstly, there was nearly no traffic as this was longer ago than I care to mention, but much more importantly, it was a hill! For me, like every kid, gears meant speed. I cared how many there were and how small that little cog was on the highest gear. Of course, the first thing I did was to climb up to the top of the hill, quickly change to the highest gear, and pedal as fast as my legs could go, clocking my speed as I went. Over and over again I sped down that hill. I remember the excitement each time I increased my record, well worth the odd grazed knee.

Fast forward to the current day and it seems not much has changed. We have just given the Volume Of Fluid (VOF) model in Simcenter STAR-CCM+ 2022.1 the equivalent of gears with the new Implicit Multi-Step method for VOF. I have been putting it to the test to see just how fast I can make free surface simulations run. 

VOF simulation speed-up using Implicit Multistep? How does it work? 

As gears decouple the speed of the pedals from that of the wheels, Implicit Multi-Step for VOF allows you to decouple the time-step at which you solve for the flow from that of the volume fraction allowing you to run your free surface simulations much, much faster. 

Traditionally in VOF, we need to set the flow time-step so that the free surface moves by less than one cell. This corresponds to a Courant number less than 1. Multi-stepping breaks that link by sub-stepping for the volume fraction multiple times within the flow time-step.  This allows you to speed-up your simulations massively by increasing the flow time-step whilst still resolving free surfaces accurately. 

The methods

There are two methods provided. Implicit Multi-Step which is new in Simcenter STAR-CCM+ 2022.1 and Explicit Multi-Step which was already in the code. We compare the approaches that these methods use with the traditional single-step approach in the diagram below. 

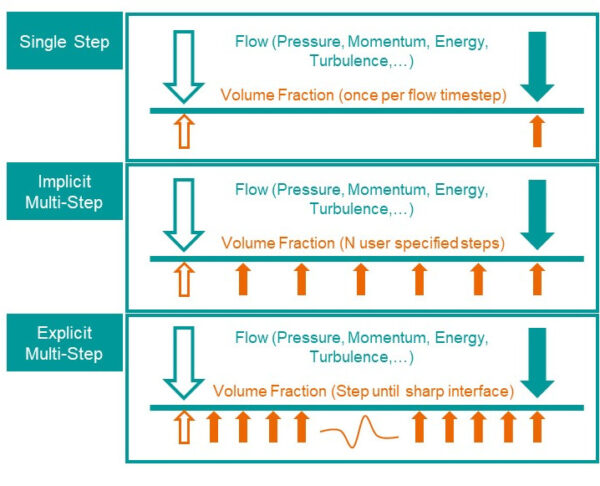
• Single step (traditional VOF) – solves volume fraction once per flow time-step 
  • If the Courant number locally exceeds 1 then the free surface will be smeared. 

• Implicit multi-step (new) solves for the volume fraction N times per flow time-step where N is specified by the user 
  • If the Courant number locally exceeds N, then the free surface will be smeared 
  • Allows N times bigger flow time-step than single-step to get a similar interface sharpness as obtained with the reference single-step method 
  • Speed up results from sub-step cost being much less than full flow time-step 

• Explicit multi-step solves volume fraction using as many sub-steps as needed to give a sharp interface 
  • Free surface must be sharp. 
  • Limiting the number of sub-steps will cause divergence rather than smeared interface 
  • Large number of sub-steps needed for sharp interface may cancel out benefits of sub-stepping in comparison to single-step case without sharp interfaces everywhere 
  • Not suited to problems with wide range of length-scales 

This is best demonstrated on an example

Our focus in this blog is the new Implicit Multi-Step. I will show the enormous VOF simulation speed-up it can bring to many applications. Let us start with a simple example that clearly illustrates the benefits – a dam break. 

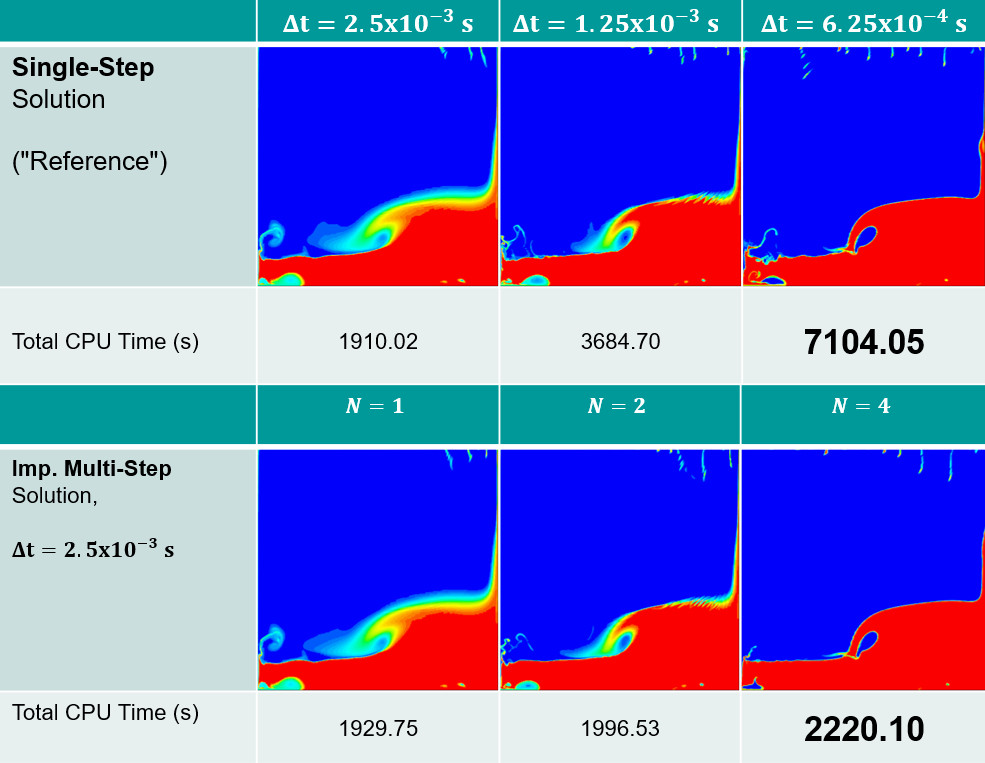
In the figure above, the top row shows the results and timings for single-step for three different time-step sizes. The results for the largest time-step (2.5 ms) show a smeared free surface. Halving the time-step (1.25 ms) improves the interface sharpness but nearly doubles the runtime and some smearing remains. Finally, halving the time-step again results in a sharp free surface but nearly double the runtime again (3.72x slower than the original time-step overall). 

The results in the second row are for implicit multi-step, but all three runs have the same larger 2.5ms flow time-step. Instead of halving and quartering the time-step, instead, we use 2 and 4 sub-steps. This allows us to use the same timescale for the volume fraction transport as the single step-runs where we reduced the time-step. The results are almost identical, but in this case, the CPU time increases by only 1.15x.

This is because the computational cost of calculating the volume fraction transport is very much smaller than that for a full flow time-step. 

As a result, by increasing the time-step by a factor of 4 and using 4 sub-steps, we can get a speed-up of 3.2x for almost identical results. 

Implicit Multi-Step for VOF simulation speed-up in action 

Let us see how much acceleration we can get on a slightly more industrial case – a tank sloshing example. This case comes from a paper with experimental data for validation of the results: Frosina, E.; Senatore, A.; Andreozzi, A.; Fortunato, F.; Giliberti, P. Experimental and Numerical Analyses of the Sloshing in a Fuel Tank. Energies 2018, 11, 682.

The tank in this example moves with a lateral sinusoidal motion. We want to see the development of the free surface and how the center-of-gravity moves with time. We can compare this with the experiment as we accelerate the simulation. This allows us to make sure we are not sacrificing accuracy (or to determine a trade-off) during our VOF simulation speed-up exercise.

The case compared here has a duration of 12s at a frequency of 0.7 Hz and an amplitude of 0.0781 m. The tank is filled with water to a level of 101 mm. To capture the free surface well, we make use of an adaptive time-step targeting the Courant number normal to the free surface (CFL = 0.34). When we increase the number of sub-steps used, we also increase the target flow Courant number in the same ratio. This keeps the Courant number associated with the volume fraction the same. 

Another gear up: A new scheme

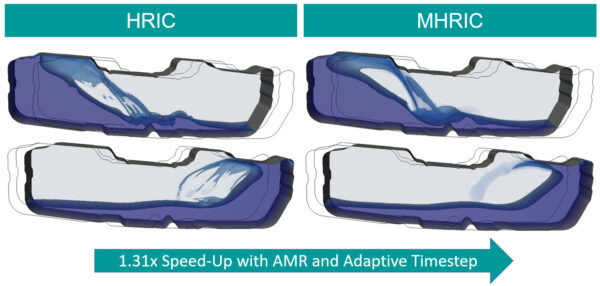
In addition to the standard High-Resolution Interface Capturing (HRIC) scheme for VOF we also test a second scheme, Modified HRIC (MHRIC) which is also new in Simcenter STAR-CCM+ 2022.1. 

We compare the two schemes below. Following the recommendations for free surface simulations, we have used Adaptive Mesh Refinement (AMR) and Adaptive Time-stepping. Looking at the results, you can see that MHRIC is a lower fidelity scheme that does not capture some of the smaller details, such as small droplets or bubbles, allowing a larger time-step. This gives us the advantage that it leads to a VOF simulation speed-up of 1.3x by neglecting details we may not be interested in whilst capturing the bulk flow features well. 

Let’s see the results

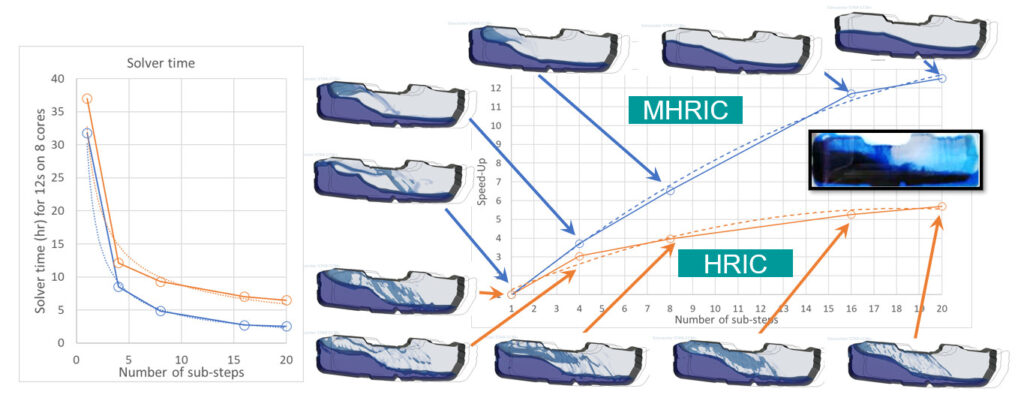
In the first set of results, we use a uniform trimmed mesh with cell size 3mm. This produces a mesh of around 1M cells. We evaluated values between 1 and 20 sub-steps on 8 cores with adaptive time-stepping but no AMR.

Let’s compare the speed-up for implicit multi-step to a single sub-step (equivalent to single-step) for both HRIC and MHRIC. This is shown in the figure below together with the flow-field results at t=7.5s. HRIC as the higher fidelity method, produces almost identical results for all numbers of sub-step tested, capturing the fine details of the flow. For HRIC, 20 sub-steps gave a speed-up of 5.7x, reducing the run time from 37 hours to 6 hours with little to no loss of accuracy. MHRIC on the other hand gives users a trade-off between speed and accuracy with 20 sub-steps giving a greater speed-up of 12.5x, but a reduction in solution quality. For MHRIC, in this case, I would argue the best accuracy-speed compromise is obtained at 8 sub-steps with a speed-up of 6.5x. 

The difference between HRIC and MHRIC is due to the cost of capturing detailed small-scale features with adaptive time-stepping. 

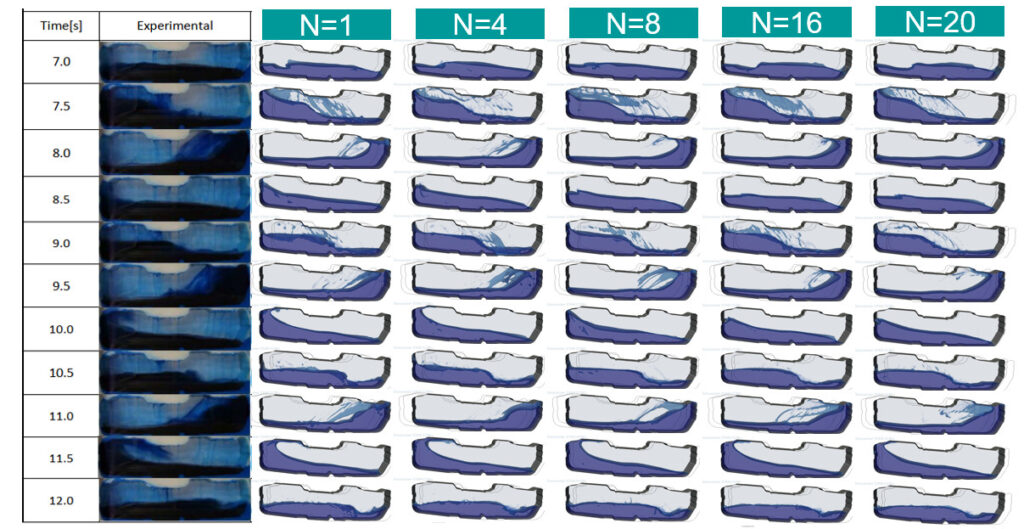
The HRIC results are shown at 0.5s time intervals between 7s and 12s compared with the experiment below:

Faster, Faster! Next gear: Adaptive Mesh Refinement!

We now get good results with a 6-hour run time, but that is not fast enough for me. So, I wanted to have another go at accelerating this case further. Next, I added free surface based Adaptive Mesh Refinement (AMR). I set this up to give the same 3mm mesh size at the free surface but a coarser mesh elsewhere. 

HRIC continues to give good results up to 20 sub-steps. The VOF simulation speed-up compared to the original case is now two orders of magnitude faster at 94x (23.4 mins). The MHRIC results show an even greater speed-up of 109x (17.5 mins). 

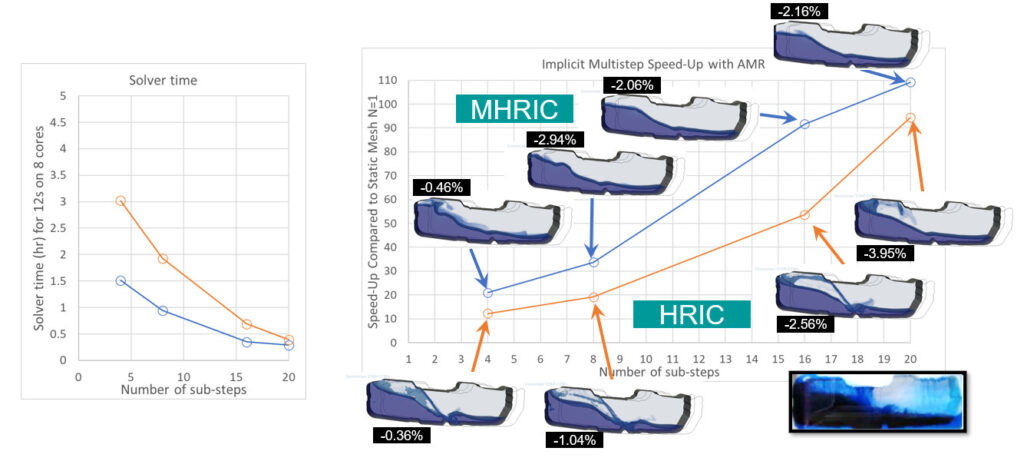
I hope you will agree with me that this level of acceleration is extremely impressive, but we are not done yet. We are running extremely aggressively, and these simulations have been set up using standard settings (5 inner iterations, default Under Relaxation Factors (URFs), default AMG set-up). This leads to some mass imbalance – these are the numbers in black boxes next to each image. To rectify this, we will carry out one more set of runs. 

Watch those knees!

The mass imbalance results from incomplete convergence during time-steps and there is an easy low-cost fix. I suggest you make a note of this recipe and use it in your applications! We need to ensure that we fully converge each time-step as we are running transiently. To do this, set URFs to 1 for all transport equations except pressure. To further ensure convergence, reduce the AMG tolerance to 0.01 for all transport equations. If we do this, we will fully converge time-steps in 1-2 inner iterations, and so we can reduce the number of inner iterations to 2. This will offset any extra cost associated with the tighter tolerance. 

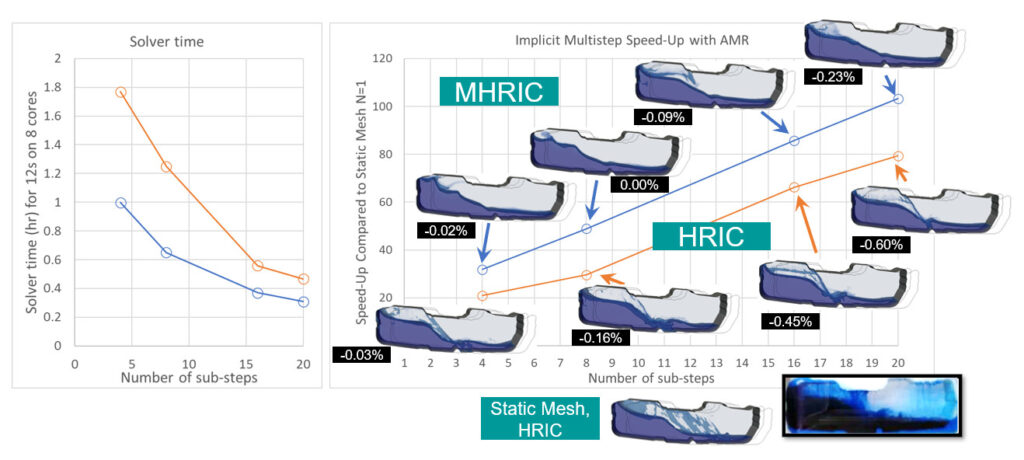
Re-running these cases gives the results below.

HRIC now gives up to 79x VOF simulation speed-up speed-up with only 0.6% mass imbalance. Whilst for MHRIC we get up to 103x speed-up with only 0.23% mass imbalance. 

Once again, I have compared the HRIC results with experiment at 0.5s time intervals between 7s and 12s in the figure below for different numbers of sub-steps:  

Based on the flow features we get a good match for all levels of sub-stepping tested. As another check on accuracy, we can compare the center of gravity of the sloshing fluid with experiment. This is shown in the plot below for HRIC for different numbers of sub-steps. We can see that up to 16 sub-steps we get a very close match with experiment based on this metric. 

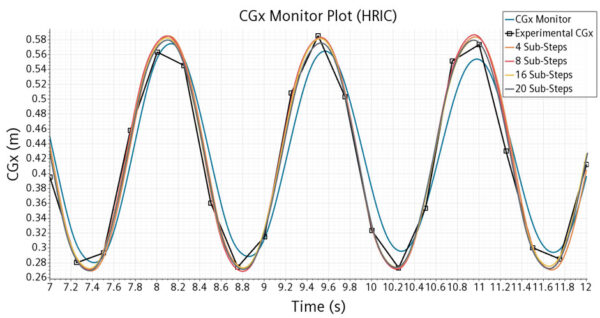
Reviewing these results, we can say that without any significant loss of accuracy, we got a 66x speed up for 16 sub-steps over the original case. What previously took hours now takes minutes! 

That’s impressive, but can’t we get more VOF simulation speed-up still? 

Like my younger self, I was having too much fun to leave it there – just one more race down the hill! How can I get this simulation to run faster still? For my last attempt, I tried a coarsened mesh.

By doing this, I could get 12s of simulated time to run in 30.5s elapsed time. The results are excellent – the mass balance is less than 1% and the Center of Gravity matches well.

From hours to seconds! Not quite real-time, but I am happy with that (for now …)!  

Without even a grazed knee, I shall now leave you to see how fast you can make your own simulations. You don’t even have to wait. Implicit Multi-Step for your VOF simulation speed-up is already released in Simcenter STAR-CCM+ 2022.1! Time to get serious in shifting gears!