The Inflowencers – Heroes of Fluid Mechanics
18th of March, 1822. Paris. France. At 37 years old, he walked into L’Académie Royale des Sciences de L’Institut de Franceon, to present something that should change the world. For the first time ever, someone had successfully included internal friction in the equations of fluid motion. It was the first time in that world that someone had described one of the most influential equations in engineering and applied physics. An equation that should become the ultimate foundation of computational fluid dynamics CFD, a discipline that should revolutionize the way products are brought to perfection.
X+Ponts man

Claude Louis Navier was an engineer. Not just any engineer but an X + Ponts: he had an education from the most prestigious engineering schools at the time, Ecole Polytechniques and Ecole des Ponts et Chaussees. As a result, he was an ultimate calculation machine, combining extraordinary analytical skills with a practical hands-on mentality. He was a remarkable combination of physicist and engineer.
In his engineering role, Navier was responsible for numerous bridge building projects. During those projects, he realized numerous deficiencies of the commonly used elastic theory of the time, which was based on an idealized fiber concept. Although he had no resolution to overcome those deficiencies at that time (1819) he had already told his students that the true foundation of elasticity should be based on molecular theory. That – for a practitioner in bridge-building of the time – was quite a disruptive thought.
And so, not resting and inspired by Laplace and Poisson’s works in May 1821, Navier was most likely the first person to derive general equations of elasticity for an isotropic body, based purely on the summation of molecular interactions. And while he thereby laid a foundation of a novel elastic theory, he did not yet take that theory into his practice. Not yet…
Instead he started pushing the envelope a bit further: The ingenious idea by Navier – and the intellectual birth of the thing later called Navier-Stokes equation was to apply his molecular technique to… you guessed it… fluids. He started looking at a fluid from a molecular perspective, and so he was the first to introduce an actually long known concept into the governing equation of fluid motion: Viscosity. As such Navier laid the foundation to finally overcome a 70 year long lasting struggle to resolve some…
Potential Problems
D’Alembert himself had rigorously proven that for any incompressible and inviscid potential flow the drag force on a body that is subject to a constant velocity flow must be zero. At the same time, everyone knew from reality that it is clearly not. It was clear that something must be wrong with the given theory of the time, something must have been missing in the governing theoretical fluid mechanics equation of the time aka Euler equation. The discrepancy became such a thing that it even received it’s own name, called the d’Alembert paradox or hydrodynamic paradox. D’Alembert himself simply said, he’d leave it to the future geometers to figure it out, nice one!
The dilemma caused headaches to some of the smartest brains of this planet at that time. Numerous legends of math including Euler himself, Laplace, Cauchy and Poisson all failed to explain the existence of a non-zero drag on any body that is subject to flow. Valid for ideal fluids, the Euler equation would not be able to explain it.
What happened after all these failures to resolve the paradox? It is like a classic you can observe even in today’s engineering world: Engineers, at the time quite successful in dealing with real-world fluid mechanics problems by using comparably pragmatic semi-empirical methods, discredited theoretical fluid mechanics as useless. And so for nearly 70 years theoretical fluid mechanics had struggled to resolve the deviation between experiment and theory due to the oversimplified assumptions of ideal fluids.
This is amazingly puzzling in hindsight as the missing piece of the puzzle had been very well know for decades. It had actually already been described by another legend – Sir Isaac Newton himself.

Trapped in the middle
Back to 1822. After Navier presented his piece of work and ultimately resolved d’Alembert paradox, what follows, is not what you’d expect. At the time this was not the birth of a legend whose equation would later rule the world of fluid mechanical engineering.
At the time – there was no fame, there was no honor, there was no believe. The hardliners of analytical math and molecular theory discredited his work as not being rigorous enough, the hydraulic engineers of the time saw no practical use to solve any relevant engineering problem.
And even Navier himself had fundamental doubts on the applicability of his equation in any real use case. Despite (or actually because of) the fact that it got rid of any ideal fluid assumptions, the equation became too complex and was deemed useless for solving real hydrodynamic engineering problems of the time. And so Navier himself put it aside. The time was not ready yet.
Heroes of Fluid Mechanics
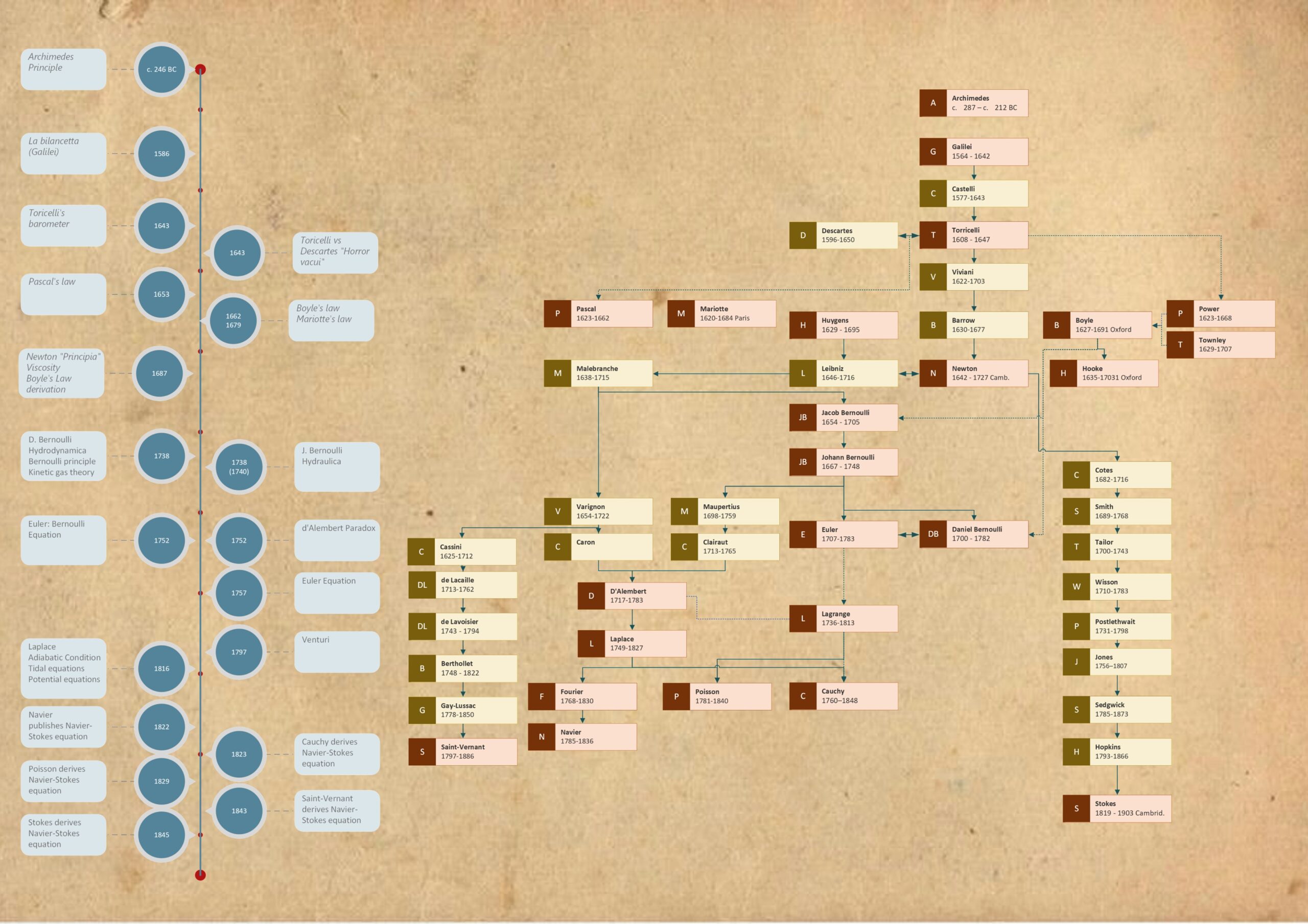
But the X+Ponts was not the first genius tumbling in the wild waters of fluid mechanics history. By the time he walked down the stairs of the academy that day, he surely was standing on the shoulders of giants. Heroes of fluid mechanics. True Inflowencers.

But like every superhero, the Inflowencers all had their Achilles heel, despite their superpowers they were, after all, just human. And like sharp rocks wait around the corner in every wild river the villains were just waiting for our superheroes to drown. And so the story of the heroes of fluid mechanics is full of instances of success and failure, honor and vanity, the purest science and the worst polemic fights, of knowledge and disinformation. Like the story of every superhero, it is the story of incredible genius and pure humanity…
So, jump on that boat with me to ride down those white waters of fluid mechanics history. And while we are rafting through the flow, be alarmed: for Navier the huge water-fall is yet to come…
Eureka

Admittedly what should soon become a wild river, starts off as a rather calm pool of water.
“Eureka!” he screamed, jumped out of his bathtub and ran through the streets of Syracuse to share his discovery. Clothes; missed in excitement. So goes the legend. Naked or not, what Archimedes discovered is without a doubt, legendary: Any object, totally or partially immersed in a fluid or liquid, is buoyed up by a force equal to the weight of the fluid displaced by the object.
But what had Archimedes been looking for? The legend says it was the resolution of a luxury problem: Uncover the impurity of a golden crown.
Centuries later, a yet unknown guy, aged 22, just dropping out of University without a degree published an essay named “La bilancetta”. The little balance was written in Italian, described a long-known instrument and at first sight did not include any experimental data to support its conclusions. Consequently, La bilancetta had not played a major role in hydrostatics at the time.
But it remains Galilei’s most underrated work for one reason: Rigorously combining theory and experiment – like in this early work- made Galileo Galilei “the father of modern physics and in fact of the whole of modern natural science” [Einstein 1933].
And the marine industry probably thinks “Eureka!”
Under pressure
As time progressed, hydrostatics got a little more intense: Pressure – a bread-and-butter concept to today’s fluid dynamicists. Yet, if you look at it with today’s knowledge of molecular dynamics, pressure remains quite an elaborate and – if you don’t know much about kinetics theory – alienating concept. And so its discovery and establishment were far from easy going and another bumpy story of fluid mechanics history.
We all know Evangilsta Torricelli came up with the first mercury barometer and was able to explain the change in the mercury level with the atmospheric pressure.
But the less famous – but actually more exciting – part of the story happened in the tube above the mercury. In the void. Where Torricelli postulated a vacuum. “If at all, the vacuum exists in his head” was (more or less) the reply by Rene Descartes – an enthusiastic fighter for the “horror vacui”, the idea that an absolute void cannot exist. It must have put Torricelli under quite some pressure.
Yet, the ultimate scientific proof of the existence of vacuum followed in November 1647 with Blaise Pascal’s experiment vide dans le vide (the void in the void).
And while this sound like nothing, it meant a lot to today’s fluid mechanics.

Mr. T’S hypothesis

Equations of state play a major role in fluid mechanics. I guess we all know the ideal gas law. We all know that pressure times volume is a constant for a fixed temperature in first approximation. And we probably know the presumable major player to come up with that fact. Now the first oddity of what is often called Boyle’s law is that it misses out on Mariotte, without whom “for a fixed temperature” would actually be missing. But even for those that believe it is correctly called “Boyle-Mariotte’s” law, be alarmed: No, it was neither Boyle nor Mariotte who originally came up with the reciprocal relation between the volume of air and its pressure. It was a guy named Townley and his mate Henry Power. The two gentleman, inspired by Boyle’s previous works, climbed British Pendle Hill to conducted an experiment that made history.
Wednesday 27th April 1661, they introduced air above the mercury in a Torricellian tube, measured its volume, and using the tube as a barometer, measured the air pressure, climbed the hill and did it again. As expected, there was an increase in volume and a decrease in pressure.
By the time Henry Power finally managed to publish the results himself (1663), Robert Boyle had already mentioned the outcome in – well – the Appendix (!) to the second edition of his New Experiments Physico-Mechanical published a year earlier. What a spoiler, you might think. Poor Power, was not even mentioned and so at the time the thing that is today called Boyle’s law (while it should actually be “Power-Townley-Mariotte’s” law) was referred to as “Mr. Towneley’s hypothesis” by contemporary authors such as Robert Hooke and Isaac Newton.
Talking of Newton..
Calculus Clash
He is a legend among the geniuses of human beings. Sure, Albert Einstein might be one-level-up in popularity, but undoubtedly this guy is playing in the same league. But as the story goes, he had not always been exactly what you’d call a British gentleman. An episode that may not directly be related to fluid mechanics still is about some fundamental mathematical principle without which, theoretical fluid mechanics and ultimately CFD would have never been possible:
No doubt the concept of calculus changed theoretical physics and math and paved the ground for modern theoretical fluid dynamics. But the “invention” of Calculus is also about two giants of science who ended up in a huge fight over an infinitesimally small element. Today we can safely assume, Newton and Leibinz came to the same mathematical concept independently. I would call it a draw.
But more importantly for a fluids-head is that one of the two gentlemen not only came up with calculus but made a visionary hypothesis on the concept of viscosity. A concept that then took almost another 135 years to be incorporated into an equation of fluid dynamics that truly closes the gap between real experimentally observable and idealized theoretical fluid behavior. A gap that had separated hydraulic engineers and fluid dynamics theorists for a long time…like calculus separated two of the biggest minds ever.
And then there is another fine detail that we as fluid mechanics or CFD engineers often tend to forget: The Navier-Stokes equation is nothing but Newtons’s second law of motion! Just with a tiny little more complicated force on the left-hand side and the addition of – yeah, guess what, Newton’s other finding: the concept of viscosity.
This guy was actually coming up with two pieces of the puzzle! No offend Mr Leibinz. But final score is 1-3.

Father vs Son

But Newton was not the only genius that could get into some beef. It could actually get even worse. Check out this one:
Imagine you and your father get jointly nominated for a prestigious prize by the French Academy of Sciences. Now, your father gets upset sharing the honor with you and did not accept that his own son was at least his equal. So, he bans you from his house.
Three years later you publish your outstanding book on fluids and in the frontispiece you state by “Daniel B., Son of Johann” to ease the trouble.
A year later your father publishes his own work which appears to have a lot in common with your book, including a quite similar title, with not a single mention of you and your work.
What would you do? Well, our hero gave up on mathematics and turned to medicine and physiology.
But, don’t you be sad! Daniel, you’re my star and the Bernoulli principle remains forever yours!
But all father vs son fight aside, although one of the Bernoullis deduced that pressure decreases when the flow speed increases, it was actually Leonhard Euler in 1752 who derived Bernoulli’s equation in its usual form.
And while the Euler equation undoubtedly was a brilliant move at the time, being among the first partial differential equations to be written down (wave equation aside) it had one major deficiency: It was only working for ideal fluids, it did not take the effects of viscosity into account.
And that brings us back to the very beginning of this story, when that 37 year old man walked down the steps of L’Académie Royale des Sciences de L’Institut de Franceon on 18th of March, 1822, with the foundation of modern Computational Fluid Dynamics in his pockets…without having a single clue what that would mean to the world one day.
Breaking Bad
Back in 1822. If after all these stories of fights and despair you now thought Navier was indeed in “good” company, well, the life of one of the biggest legends of fluid mechanics was about to get a lot more tragic.
While in doubt on his works on fluid mechanics, he finally took a bold move on the Mechanical Engineering side of things: It was when the City of Paris decided a new prestigious passenger bridge was to be built across the river of Seine. Navier, who had by this time had studied state-of-the art suspension bridges intensively, raised his hand. But building the bridge in the old-school engineering way, was no longer good enough for the X + Ponts. The X was calling:
And so, in 1823 Navier presented a plan for the Pont des Invalide, an elegant steel bridge that should become the first rigorously designed by the principles of theoretical elasticity analysis.
It was the leap of faith to apply his theoretical works to real life engineering that he never seemed to have dared or considered to apply for fluid dynamics. And he should pay for that bold move. When the bridge opened everything about Pont des Invalide was designed based on a Navier’s theoretical analysis. When he presented his plans for the bridge the committee of experts reported very favorably on Navier’s project, convinced that “theory everywhere illuminates practice.” Based on his previous works on elastic theory Navier now had sufficient confidence.
Too much confidence maybe. Because he made a fundamental mistake: In his firm believe in rigorous math he neglected the common engineering practice of a safety margin. There was no safety multiplier in his structural strength calculations.
In August 1824 the building began. Elements of his bridge design were novel and untried, and neither did Navier test those on a scale model, nor did he “overbuild” to compensate for possible error.
And so when the bridge was almost complete, on the night of 6th to the 7th September 1826 a broken water pipe ended the dreams of Navier’s revolutionary mathematical engineering for bridge building. A broken water pipe (!), indeed, fluid dynamics! On that night water from a nearby pumping station flooded the earth surrounding on of the buttress of the bridge. And it cracked…
For a moment it looked like an engineering approach based on rigorous theoretical grounds had experienced a major set-back, it looked like the incredible achievement of overcoming d’Alemberts paradox would remain the useless pet of some over-thinking theorists, and it looked like the father of CFD’s governing equation stumbled over a bridge breaking bad.
But you can’t keep internal friction from resurfacing…
Internal Friction- The Navier-Stokes-and-the-three-other-guys-Equation

And while he was breaking bad on the mechanical side, things were not all roses on the hydrodynamics front for Navier either. While stuffed with ingenious ideas – Navier’s derivation of the fluid mechanics equation was not above and beyond all doubts – at least not at the time. And not in the eyes of a radical supporter of a rigid molecular approach: Poisson.
Presumably triggered by Navier’s memories, the Laplacian hardliner came up with something that can be considered a rework of Navier’s but with significant differences in underlying assumptions and methods. While at it, Poisson dismissed Navier’s work as in his view it was derailing from first molecular dynamics principles when substituting molecular sums by integrals – a no-go for Poisson. It culminated in a yearlong polemic fight between the two gentlemen. (It is interesting to note that Navier and Poisson were actually on the same page with respect to the importance of a discrete treatment of matter as molecules and their interaction, they ended up with similar equations, and yet the devil in the details of their assumptions caused such a massive dispute.)
And for Poisson it was not the only dispute. At the same time he dismantled Navier’s work, he found himself in a race with Cauchy, who – like the two other gentleman – searched for a sound elasticity theory, started from a molecular perspective, introduced “non-normal/tangential pressures” (today known as shear stress), introduces some concept of momentary stresses and – almost like a collateral – ended up with a governing equation for fluid motion – that resembles Navier’s equation. The competition between Cauchy and Poission was so intense that Cauchy deposited a draft of his work at the French academy of science before he published it years later (likely in respect for Navier’s work) and Poisson read his memoires in unripe form before he officially finalized his work in 1829.
And while Cauchy, Poisson and Navier held their dispute on fundamentals, another X+Ponts, entered the stage stimulated by Navier’s failed attempt to build a bridge based on rigid mathematical principles. Saint-Vernant, fluent mathematician and excellent engineer. He was the type of guy it need to close the gap between pragmatic engineering and sound theoretical derivations, between a molecular perspective and an applicable continuum view for a hydrodynamics equation. “My principal goal is all practical” said Vernant while he always avoided a too narrow empricism.
In his unique style, Siant-Vernant conceptually separated the translatory motion observed in hydraulic experiments from an invisible non-translatory motion that molecular interactions necessarily implied. He further postulated that macroscopic motion diminishes at the price of hidden microscopic motion. What he ended up with in 1843 is – you guessed it- Navier’s equation.
But while the rest of the Fab4 were spending their time fighting over details in the molecular interaction, Saint-Vernant focused on pushing the envelope on the application side. He started applying the eqution to channel flow, revisits d’Alembert paradox and resolved it by taking into account work related to internal friction. He thereby postulated that the higher the non-translatory amount of motion the higher the resistance and that with a very large increase in “tumultous”, whirling motion compared to “smooth flow” the resistance increases significantly. And while at it, Saint-Vernant was the first to apply the strategy of reinterpreting Navier’s hydrordynamic equation as controlling the average smooth flow with a variable viscosity coefficient. (a concept that should become so fundamental to CFD as the equation itself.)
Stoked
But these four Frenchman should not be the end of the story. Obviously we still lack of one name-giving protagonist. Until 1845 it was an all French-game. And then entered the stage – you guess it – Sir George Gabriel Stokes – a brilliant mathematician and experimenter. He brought to the table, what – in all his excellence and despite his experience as a practitioner – Navier maybe lacked of: an Experimental mindset: Stokes was the first to take experiments into consideration to quantify the imperfection of fluids and relate those insights on internal friction back to the fundamental equation of hydrodynamics.
In 1845 he published his work on the friction of fluids in motion and the equilibrium and motion of elastic solids. It is this work where the Navier-Stokes equation sees the day of light for a fourth time. The second major contribution follows five years later with Stokes work on the effects of the internal friction of fluids on the motion of spheres, disks and cylinders. In rigorous mathematical fashion, he managed to start from his generalized equation, boil it down to cases that he could handle analytically and compare his theoretic results to numerous existing experiments on pendulums with oscillating spheres and cylinders of all sizes in all sorts of fluids. All this without assuming ideal fluids, i.e. considering a thing he labels the index of friction.
Ultimately, his work allowed him to calculate the final velocity of a sphere falling in a viscous fluid, thereby deriving an expression and establishing the concept of drag force. It was the down to earth, rather practical manifestation of the theory of non-ideal fluids. The final missing step in the effort started by Navier more than twenty years earlier. It was the breakthrough to a more practical relevance of the theory that would then become the Navier-Stokes equation. The only elephant in the room, keep the velocities involved low enough…

Turbulent times ahead
Archimedes, Galilei, Torricelli, Pascal, Boyle, Mariotte, Townley, Power, Newton, Bernoulli, Euler, d’Alembert, Cauchy, Poisson and Saint-Vernant … this crew had rafted a wild ride. A ride of passion and ingenuity and with significant impact on the two gentleman to come: Thanks to all their inflowencers, Navier and Stokes ultimately rocked the boat. And yet, they never saw the impact their findings made on today’s engineering.
And while they went into history as the fathers of a legendary equation, it was only just the beginning. Because in the river of fluid mechanics history, the turbulent passages were yet to come…
… to be continued

Acknowledgement
I would like to thank Olivier Darrigol for being such an amazing source of inspiration. The idea to this blog was above all triggered by and many insights gained from his incredible book Worlds of Flow: A History of Hydrodynamics from the Bernoullis to Prandtl
References
The Paris Bridge That Never Was. Norman Ball.Posted on April 20, 2014 by Parisian Fields
“On the theories of the internal friction of fluids in motion and of the equilibrium and motion of elastic solids”. Stokes, G.G. (1845). Transactions of the Cambridge Philosophical Society. 8: 287–319.
“On the effect of internal friction of fluids on the motion of pendulums”. Stokes, G. G. (1851). Transactions of the Cambridge Philosophical Society. 9, part ii: 8–106. Bibcode:1851TCaPS…9….8S. Orig
Comments
Comments are closed.



I liked to read this blog. Thank you!