Efficient and Accurate Broadband FEM-based Vibro-acoustics (Part 1)
Challenges of vibro-acoustic FE modeling
CAE simulation fundamentally virtually simulates the behavior of continuous or “infinite” objects subject to various physical forces into discrete or “finite” elements. By breaking down the problem into finite elements we are able to numerically approximate the real behavior. However if your approximations are too coarse, you can get erroneous results but if they are too fine it could be computationally-intensive not to mention cost-prohibitive. Therefore we must always strike a balance and modeling finite elements this can be achieved by either controlling the size & number of elements (mesh refinement) or by controlling the element order.
The Finite Element Method (FEM) is well established for the prediction of vibro-acoustics engineering phenomena across the board, ranging from automotive to mechanical to naval applications (see figures below). The classical FEM however suffers from several issues to efficiently tackle vibro-acoustic problems.
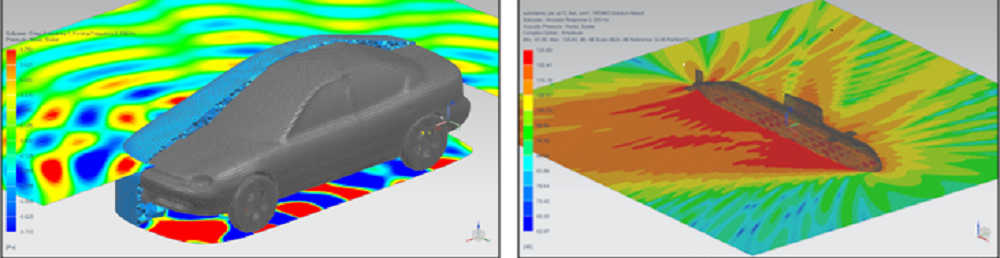
Left: Full vehicle exterior acoustics, panel loading due to tire/tailpipe noise Right: Submarine sonar scattering
First, the mesh size is defined for a given target frequency, such that in theory, a different mesh should be prepared for each frequency of interest. In practice, this is rarely performed, as this proves very demanding for engineers. Instead, it is common practice to define a single highly refined mesh, designed for the highest frequency of interest, to cover a large frequency range. The problem with this approach is that while it may be relatively straightforward to setup there is a huge increase in the computational cost required to solve such large refined meshes, and can become impractical.
Secondly, these practical considerations are subject to a more fundamental limitation of the conventional finite element methods at higher frequencies. In particular, the pollution effect (which can be described as the cumulative build-up of dispersion error over the computational domain) leads to a rapid increase in numerical error at high frequencies. This exacerbates even further the differences in mesh resolutions required for low and high frequencies. Finally for exterior acoustics, an additional challenge is the “infinite” size of the exterior radiation domain, which is difficult to manage with conventional low-order FEM.
FEMAO: Automatically adapting element order
In Simcenter 3D Acoustics, two key innovative technologies are included to help you master the mesh complexity for your vibro-acoustics applications: Finite Element Method with Adaptive Order (FEMAO) and Automatically Matched Layer (AML).
The first key technology we will discuss this week is the Finite Element Method with Adaptive Order (FEMAO) in which a high-order polynomial FE method is used in conjunction with an automatic a-priori error indicator. As mentioned earlier there are two methods by which we can control an FE mesh, by refining the mesh or controlling the element order. The challenge with the first approach is it is highly dependent on the 3D geometry which may not be able to accomodate such refinement.
FEMAO addresses the second approach by adapting the element order; in this case engineers only need to input a single coarse mesh and a desired accuracy, and the solver automatically selects the element order at each frequency so as to obtain a target accuracy while minimizing the cost. An optimal model size is hence obtained for each frequency, allowing to perform the broadband vibro-acoustic analysis optimally on the full frequency range with a minimal user intervention (see figure below).
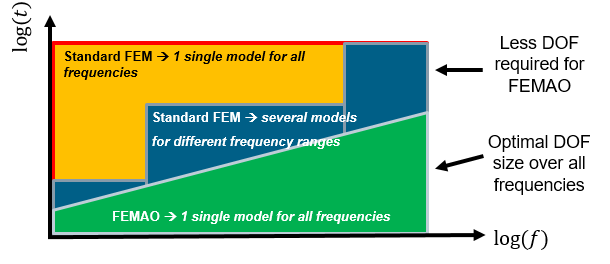
One-size fits all approach with FEMAO
Standard FE Method vs FEMAO Method Comparison
For a representative interior vibro-acoustics case in automotive industry, the figures below compare the classicalFEM mesh tuned for a certain frequency limit and the FEMAO mesh for the same frequency limit.
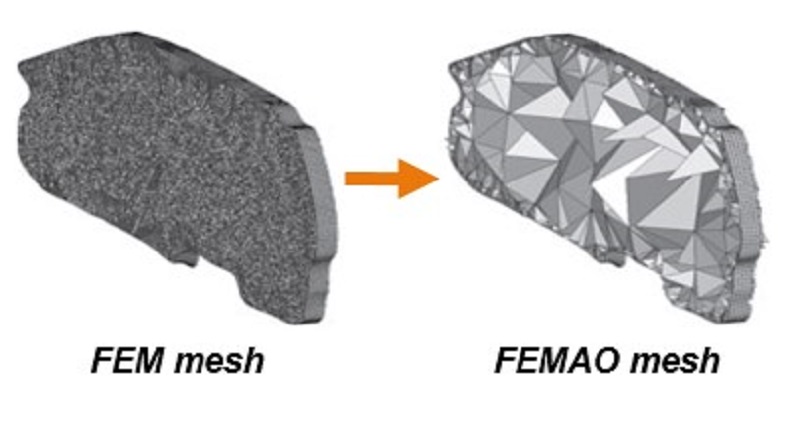 Classic refined mesh vs FEMAO method
Classic refined mesh vs FEMAO method
When comparing the frequency vs. solution time curve between the classic FE model (in blue) vs the three FEMAO models (orange, yellow & purple) shows that:
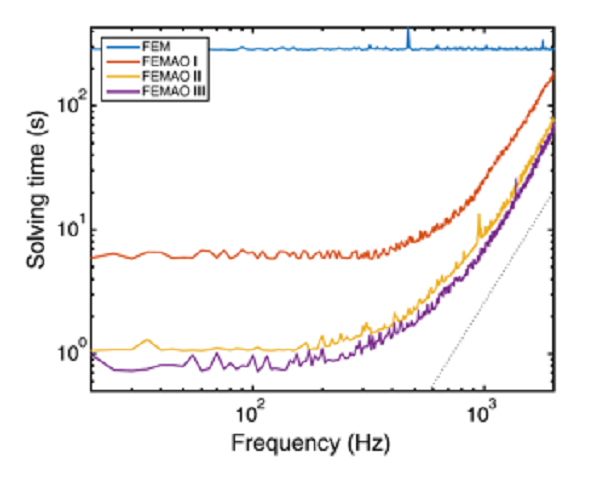
Solve Time vs. Frequency Classic FEM vs FEMAO
-
- At lower frequencies: FEMAO solves orders of magnitude faster due to the combination of a coarse mesh with a low element order, yielding a very efficient prediction model.
-
- At higher frequencies: FEMAO is also more efficient with the solving time for FEMAO still factors lower than standard FEM.
Summary
This innovative technology is the result of in-house research work at Siemens PLM Software together with leading academia, in close collaboration with end users for methodology validation on their cases of interest. In particular,
-
- FEMAO was developed as part of an EPSRC-funded Engineering Doctorate programme together with the University of Southampton [1];
Next week we will discuss the other fundamental technology that transforms vibro-acoustic analysis, the AML (Automatically Matched Layer).
[1] “Bériot, H., Prinn, A., & Gabard, G. (2016). Efficient implementation of high‐order finite elements for Helmholtz problems. International Journal for Numerical Methods in Engineering, 106(3), 213-240.”