Geometric Constraint Solving: introduction

Organizing shapes in 2D designs and 3D models
Geometric Constraint Solving has been a hugely successful approach for organizing shapes and structures in space in the digital world. It’s fundamental to modern design applications and is widely used to make 2D sketching and 3D modeling more intuitive and practical for designers.
Geometric Constraint Solving is, however, very difficult – we’re still making enhancements to our own technology after 30 years. Fortunately for users of design software, all of the complex math problems are solved under the hood.
In this article, we’ll introduce the fundamental concepts for organizing shapes and structures in design applications, and review where geometric constraint solving is used.
Let’s begin by defining a few terms:
| Term | Description | Examples |
|---|---|---|
| geometric entity | Basic building block in a 2D sketch, or a 3D model | point, line, circle, ellipse, cylinder, sphere, torus, … |
| dimension | Measured quantity assigned to a geometric entity, or between geometric entities | radius, distance, angle, … |
| constraint | Logical rule (yes/no) that is assigned between geometric entities | tangent, perpendicular, symmetric, pattern, … |
What is geometric constraint solving?
Following from the definitions above, Geometric constraint solving enables designers to create and modify a 2D sketch, or a 3D model, in such a way that it should satisfy any dimensions and constraints that the user has assigned to the constituent geometric entities.
As a result, geometric constraint solving offers the following key benefits:
- Designs can be specified with a very high degree of accuracy, limited only by the resolution of the host computer.
- Design variations can be explored easily. For example, by modifying particular dimension values, or by moving geometric entities. Satisfying all other dimensions and constraints simultaneously ensures that the design intent is preserved.
In the figure opposite, the value of a distance dimension is being modified to drive a rapid design change in the 3D model.
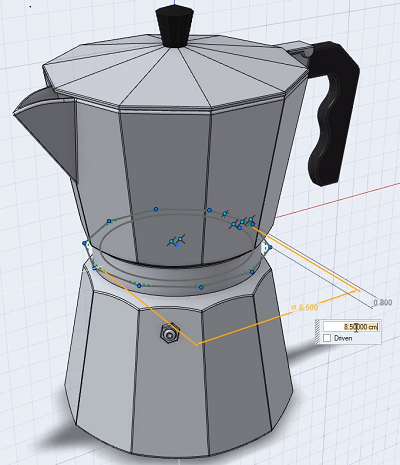
Where is geometric constraint solving used?
The key benefits of geometric constraint solving are mostly realized in Computer-Aided Design (CAD) software across all sorts of industries: automotive, aerospace, consumer products, architecture, etc. This is because the technology is well-established in improving productivity in the design process. CAD software vendors who license our D-Cubed geometric constraint solvers include Autodesk, DataSolid, Fujitsu, IronCAD, ISD, Onshape, PTC, Top Systems and ZWCAD.
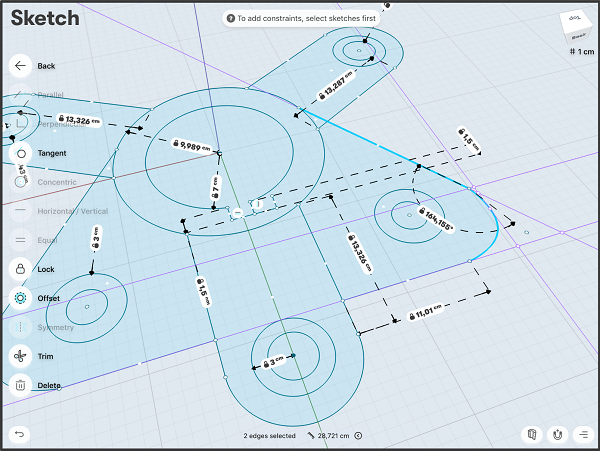
Dimensions and constraints capture the design intent accurately in a CAD sketch in Shapr3D. Read the full case study here.
In Computer-Aided Engineering (CAE), product designs can be systematically modified using geometric constraint solving to iterate variable dimension values, simulate the resulting geometry and target the optimal part shape. CAE software vendors who license our geometric constraint solvers include Altair, ANSYS, Autodesk, AVL, COMSOL, ESI , MSC.Software and Remcom.
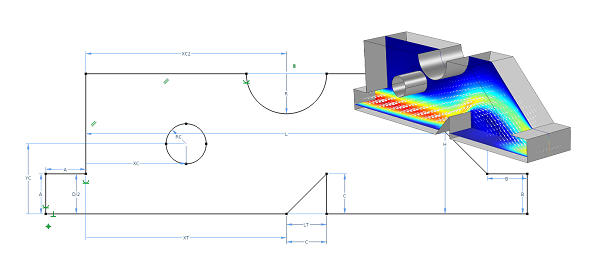
Parametric optimization of fluid flow in a part using COMSOL software; design variations are explored using the D-Cubed 2D geometric constraint solver. Read the full case study here.
Computer-Aided Manufacturing (CAM) software also adopts geometric constraint solving. In doing so, manufacturing experts can make design tweaks that support optimal manufacturing processes while paying attention to the original design intent. CAM software vendors who license D-Cubed geometric constraint solvers include Autodesk, Euklid CAD/CAM and Vero Software.

3D geometric constraint solving can be used to position parts in a manufacturing mold
In Architecture, Engineering and Construction, geometric constraint solving may be used to manage parametric floor plans, or the relative positions of architectural features in a building. AEC software vendors who license D-Cubed geometric constraint solvers include Autodesk, Bentley and Nemetschek Vectorworks.
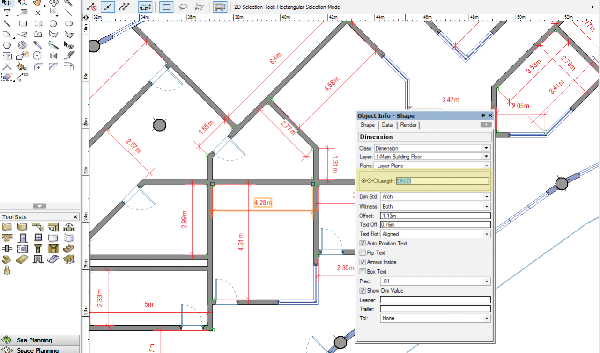
2D geometric constraint solving for positioning walls in an architectural floor plan
Solving a complex problem universally
If geometric constraint solving is so difficult, how has the solution become so universal? The evolution of history-based modeling offers part of the explanation. By the mid-1980s, several major mechanical Computer-Aided Design applications were adopting history-based modeling in which 3D models are defined by a sequence of operations. For example, a very simple 3D model might be defined with the following steps:
- Create a closed 2d sketch with dimensions and constraints that define its shape
- Extrude the sketch by distance x into a 3-dimensional solid
- Sweep a hole through the 3D solid
- Create a cylinder that is concentric with the hole to represent a shaft
The model would be stored as a series of operations and associated parameters (dimensions and/or constraints) which could be replayed to reconstruct the model unambiguously in a new modeling session. The parameters could also be modified to rebuild new design variations.
Geometric constraint solvers offered the solution for solving parameters in history-based modeling which comprised dimensions and constraints – either in a 2D sketch, or between 3D parts.
By the end of the 1980s, the private company D-Cubed was established by Dr John Owen in Cambridge, UK to focus exclusively on the geometric constraint solving problem. The company’s solutions, D-Cubed 2D DCM and 3D DCM1, were packaged as software components for geometric constraint solving in 2D and 3D respectively that could be licensed by any software vendor. Many vendors in CAD, AEC, CAM, CAE chose to eliminate the risk and cost of developing their own solvers by adopting the D-Cubed components. The D-Cubed software team and their technologies were ultimately acquired by Siemens Digital Industries Software, who continue to make the geometric constraint solving components openly available to other software vendors.
In addition to 2D sketching and 3D part positioning, new applications have emerged for solving geometric constraints, including direct 3D part shape modification and parametric 3D routing.
In conclusion
Geometric constraint solving has been integral to applications across design, simulation and manufacturing over the past 30+ years to bring significant productivity advantages. Many of the leading applications in these domains use D-Cubed geometric constraint solvers.
Further information
Footnote
1 DCM is an abbreviation of Dimensional Constraint Manager. A dimensional constraint is a rule pertaining to the size and/or shape of a design. Distances and angles are examples of dimensional constraints. In the 2D DCM and 3D DCM product names, the prefixes 2D and 3D are referring to the number of dimensions of mathematical space in which dimensional constraints are being managed (solved).


