Response Surface and Sequential Optimisation of a Heatsink Using FloTHERM. Part 2 – Design of (Computational) Experiments
The most effective, but least efficient, method to determine an optimal combination of design parameters is to consider every single possible combination of them and to then observe which combination best achieves the design goal. For smoothly varying design parameters this would entail the need to investigate an infinite number of combinations. Who’s got time for that? A sub-set of combinations needs to be identified that provides enough insight so that the optimum can be inferred via some type of interpolation. This is where a Design of Experiments (DoE) approach comes to bear.
There are various ways in which this sub-set of combinations can be determined. If ‘M’ step changes are considered in each of the ‘N’ design variables (degrees of freedom) a full coverage would result in M^N combinations. In this heatsink example, a modest 10 steps of each design parameter would result in 1000 FloTHERM simulations being required.
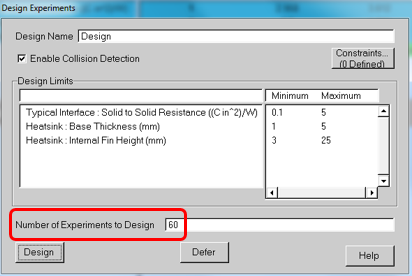 FloTHERM’s DoE technology takes a user defined number of combinations and distributes them throughout the design space. The distribution itself is automatically determined using an optimisation that distributes the points so that there is as equal a distance between them as possible. In 1D this is easy to achieve. In N dimensions it is a more complicated calculation, but no more difficult than pressing a button in FloTHERM. The resulting combinations can be visualised as 2D projection scatter graphs:
FloTHERM’s DoE technology takes a user defined number of combinations and distributes them throughout the design space. The distribution itself is automatically determined using an optimisation that distributes the points so that there is as equal a distance between them as possible. In 1D this is easy to achieve. In N dimensions it is a more complicated calculation, but no more difficult than pressing a button in FloTHERM. The resulting combinations can be visualised as 2D projection scatter graphs:
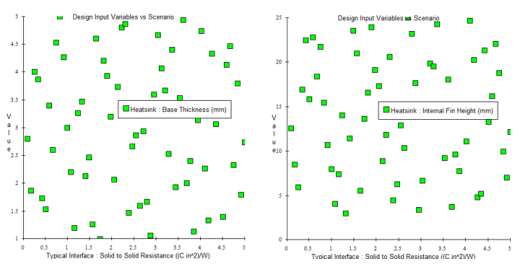
If you think the distribution looks less than equal, remember that these are projections from points equally distributed in 3D. The more degrees of freedom there are, the less equally distributed they will look after projection.
A scenario of ready to solve FloTHERM projects are created in Command Center. These can be individually inspected before they are solved. Here cycling around the first 13 combinations (note that two of the degrees of freedom are geometric in nature, the 3rd is implemented as a parameter (area normalised interface thermal resistance) ):
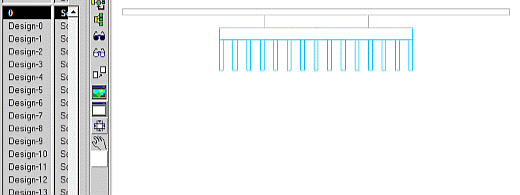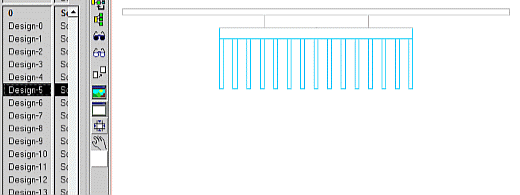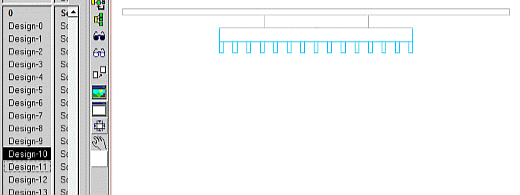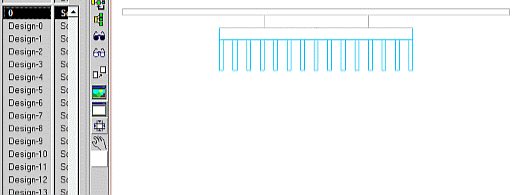
So, the question is begged “how many combinations are required to get enough insight into the relationship between these degrees of freedom and the design goal?” To answer that we’ll look into cost function response surfaces next time.
1st February 2016, Ross-on-Wye