How much do ‘U-Value’ good thermal insulation? Part V
Why is it that when you increase a cavity air gap size beyond ~30mm is there no subsequent detrimental affect on the overall U-Value? Why is it that the U-Value of the cavity gap nearly doubles when the air gap reduces to such as size so as to stagnate the air? Questions that come begging after observing the FloVENT simulation results discussed in the previous blog posting. Let’s find out….
When I started this blog I had some pretty conceited expectations as to what I would find out. You never learn anything by getting things right first time. Stagnant air is a great insulator, moving air isn’t. So why is it that when the cavity air gap size reduces does the overall thermal resistance (R-Value, inverse of U-Value) decrease? The answer is in the gap size. A conductive thermal resistance = d/kA, where d is the length the heat flows, k is the thermal conductivity of the material through which it flows and A is the cross section area of the heat flow. Stagnant air might have a low k but to achieve stagnation you have to have a real small d. So small in fact that the overall thermal resistance is much smaller than when you have a bigger gap and moving air (which has a much higher effective thermal conductivity).
It’s often good to think of moving air as a solid object but with a very high thermal conductivity but you have to be careful about what subsequent insights you gain from such a convective->conductive analogy. Heat that flows (due to conduction) in a material with an isotropic thermal conductivity (same in all directions) will always flow in the direction of the temperature gradient imposed across it. When looking at heat flow in fluids (convection) the heat flows predominantly in the direction of the air flow. [A more involved definition would get into Peclet number; which this isn’t; so it won’t]
To better understand the physics of the air and heat flow in the cavity the following figure shows what’s going on as the gap size goes from 1mm right the way up to 100mm. It only shows a small vertical section of the wall, about half way up. Both air speed and heat flux are represented by arrows. The size of the arrow represents the magnitude of the air speed (m/s) or heat flow (W/m²).
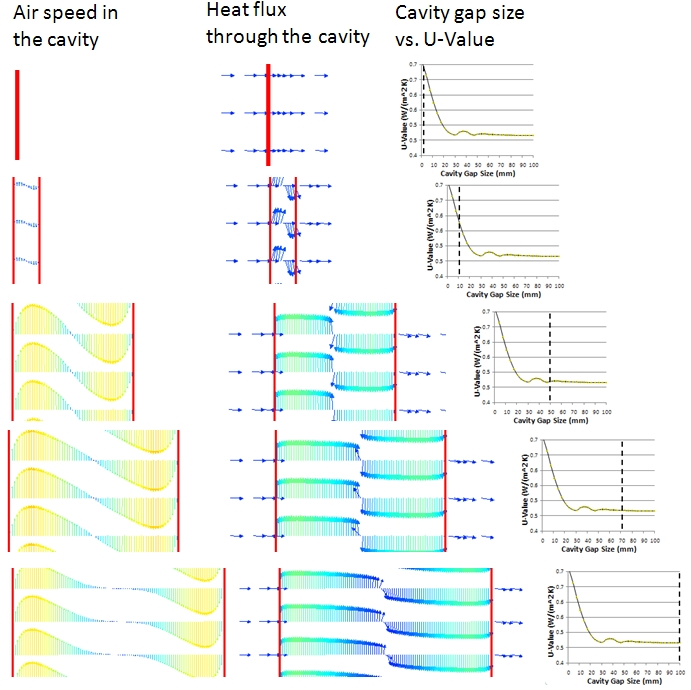
For the smallest air gap the air is not moving, the heat flux passes through the gap as if it were completely solid. As the gap size increases to 10mm the air starts to move albeit very slowly. Instead of the heat passing perpendicularly through the gap the air takes some of the heat upwards, turns round at the top of the cavity (not shown) and passes back down the outer wall where it then conducts outwards. Some of the heat still conducts through the air, some is convected around in a big loop. The net effect is for the heat flux arrows to be angled to the right, upwards due to convection, left to right due to conduction. From 50mm and above all the heat is transferred by convection. The heat flux vectors all point in the direction of the air flow.
Going back to the ‘moving air can be viewed as a solid with a conductivity’ analogy, the conductivity is such that it is high in the direction of air flow. Instead of the heat passing left to right through the gap when the gap is very small, when the gap increases so that the air can move, it has to travel all the way up one side of the cavity and all the way down the other. The overall distance the heat travels is not the gap size, it is effectively twice the room height. Viewing air as a solid with a conductive resistance = d/kA, the d is now very big, the A is now half the cavity plan area and the k (by some rough and ready observation looking at the W/m² in the air flow and the temperature gradient in the air flow direction) comes out at about 10,000 times higher than when the air is stagnant. So, even though moving air has a very high effective thermal conductivity, the overall thermal resistance increases because the increased distance and reduced cross sectional area the heat has to travel through are more dominant factors.
OK Robin, you’ve just about managed to ramble through your explanation as to why the thermal resistance increases (U-Value decreases) once the gap is big enough for the air to start moving. What about the fact that beyond ~30mm gap size the overall thermal resistance does not alter, what say you to that?
Let’s carry on with this conductive analogy. This big loop the heat travels along, up one side, down the other; once the gap size increases beyond 30mm the maximum air speed in the cavity does not increase. This can be seen from the final three air speed vector plots in the above figure. There is stagnant air in the middle of this recirculation come a 100mm gap but so what, the heat is still going up one side and down the other. The total distance the heat travels is about the same give or take the 180degree turns at the top and bottom of the cavity.
Convection and conduction are not the only ways in which heat can pass through the wall construction. Radiation has had a bad press (for obvious reasons) but when it comes to radiative heat transfer it’s something that can play a very important role. More on that next time!
2nd March 2010, Nottingham