Multiscale Analysis: A General Overview and Its Applications in Material Design
Multiscale modeling is a broadly used term. It can be used to describe any situation where a physical problem is solved by capturing a system’s behavior and important features at multiple scales, particularly multiple spatial and/or temporal scales. Applications for multiscale analysis include fluid flow analysis, weather prediction, operations research, and structural analysis, to name a few.
Multiscale Analysis of Advanced Materials
Modeling advanced materials accurately is extremely complex because of the high number of variables at play. The materials in question are heterogeneous in nature, meaning they have more than one pure constituent, e.g. carbon fiber + polymer resin or sedimentary rock + gaseous pores.
While heterogeneity offers huge advantages in performance (making airplanes, space shuttles and lightweight cars possible), it also introduces difficulties in the engineering design. Presently, there is not enough computational power to include all the important details within a single Finite Element (FE) model, as is customary in industry. This is because that would require a high-resolution model too complex to be feasibly solved.
While the simulation and analysis technology for metal structures such as car frames is quite robust, the analysis of novel “advanced materials” is lagging. The consensus is that by using conventional techniques (standard FEA) it is not possible to accurately simulate these materials without extensive experimental and empirical “calibration” data. Thus, the introduction of new materials into a structure results in increased time to market and costs.
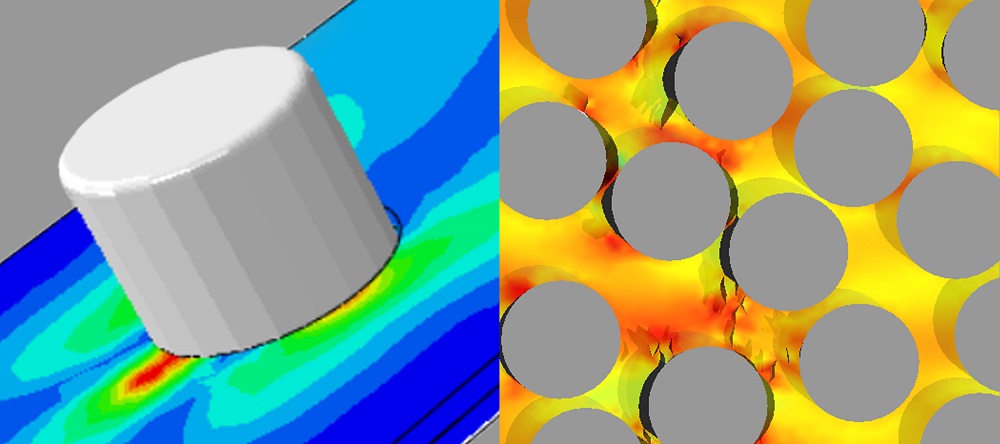
The most efficient solution is to use multiscale FEA to divide and conquer the problem. To accomplish this, a local scale model of the material microstructure is embedded within the global scale FE model of the part. Then, the software analyzes the different scales simultaneously. The behavior of one level affects the behavior of the other.
Solving each scale individually and linking their results is much faster than trying to solve a single high-resolution model containing all relevant details. However, not all multiscale techniques are alike.
The goal of multiscale simulation is to achieve balance between simulation accuracy and computational efficiency. For this reason, there are several different types of structural multiscale analyses that attempt to strike that balance:
- Multiscale with analytically modeled microstructure
- FE^2
- TRUE Multiscale
Analytically Modeled Microstructures
One technique used to account for microstructural nuances is to use an analytical equation to model behavior. Engineers develop these equations empirically by witnessing controlled experiments. Then, they generate a relationship between all relevant variables that match the observed outcomes.
We define semi-analytical methods as direct micro/macro procedures for which the local constitutive equations and criteria are evaluated at the local scale and explicit relations are used to establish the link between the macroscopic behavior with microstructural responses.
Some of these techniques aim to homogenize the properties of the local scale; others attempt to capture nonlinear behavior via curve fitting and progressive damage approaches. Many of the most famous techniques, such as those evaluated in the World Wide Failure Exercises, are related to the analysis of unidirectional composites. There are others that relate to spherical or oblong inclusions. The key is that the user must be very aware of the assumptions and bounds of their model when employing one of these techniques.
These methods are certainly more accurate than their single-scale, isotropic predecessors, but fall short when trying to analyze novel parts/materials for which there is no historical correlations or empirical guide-posts.
Finite Element Squared (FE^2)
FE^2, introduced by Feyel in 1998, describes the behavior of heterogeneous structures by using finite element models at both the global and local length scales. At each integration point at the macroscopic scale, the software assigns a representative volume element (RVE) and simultaneously performs a separate finite element computation. Next, the macroscopic behavior is thus deduced from the nonlinearities in the behavior of the associated microstructure. Then, the software builds a model using three main ingredients:
- A modeling of the mechanical behavior at the lower scale (the RVE)
- A localization rule which determines the local solutions inside the unit cell for any given overall strain
- A homogenization rule giving the macroscopic stress tensor, knowing the micromechanical stress rate
Because the microstructure is a finite element mesh, all standard analysis techniques, failure theories, constitutive models, etc can be easily applied. For this reason, FE^2 is flexible and highly accurate, but many companies consider it too expensive to be practical in full component designs and optimizations. In cases where nonlinearity is modeled, it is as if the number of computations required for standard FEA is being “squared.”
True Multiscale
True Multiscale was developed and used exclusively at Siemens Digital Industries Software. It combines the accuracy of FE^2 with the computational efficiency of analytical methods. True Multiscale is as accurate, if not more so, than FE^2. It also enable 1,000x gains in efficiency.
Similar to FE^2, this approach allows one to explicitly model microstructural details, capture local progressive damage, and show the coalescence of local scale phenomena into global scale phenomena. In other words, the approach naturally inherits the same amount of flexibility and accuracy found in the widely accepted FEA and FE^2 methods.
With this approach, engineers are able to perform component and subcomponent designs with production-quality run times, and can even perform optimization studies.
To learn more about how you can integrate True Multiscale technology in your engineering workflow, click here.


