Accounting, AI and floating point
Most people, when they think about numbers, mathematics or science, are thinking about precision – getting exact answers. However, I have observed that, in many fields, this may not be a clear perception. For example, in accounting it is expected that a balance sheet will – er – balance; it must be penny perfect. On the other hand, accruals are just a “best guess” and precision is not expected. Likewise in science. Some research is looking for tiny differences in a signal. I am thinking of gravity wave research and the SETI program. Other areas of research, like quantum physics for example, is all about statistics and absolute precision is, by definition, impossible.
So, what has this got to do with AI and embedded systems? …
Most software operates using one or both of two kinds of numbers: integers or floating points. Integers have the benefits of being easy and fast to process and having absolute precision; their downside is their overall range is somewhat limited. They should always be the first choice for any application, if they fit the bill. Floating point, on the other had, has well-defined precision and normally a very wide dynamic range, but is slower to process. However, certain applications really benefit from floating point, so some understanding of how it works is useful.
The usual floating point format is defined by the IEEE and is called fp32. As the name implies, it is a 32-bit object, where the bits are utilized thus:
- 1-bit sign
- 8-bit exponent
- 23-bit mantissa
The number is simply the mantissa multiplied by 2 to the power of the exponent. This gives a wide range and good precision. If speed is not essential, fp32 is very useful. Even though dedicated hardware can help, processing fp32 data is time consuming.
If higher performance is needed, there is fp16, which is a 16-bit object with lower precision and restricted range, thus:
- 1-bit sign
- 5-bit exponent
- 10-bit mantissa
A significant problem is that conversion from fp32 to fp16 is difficult.
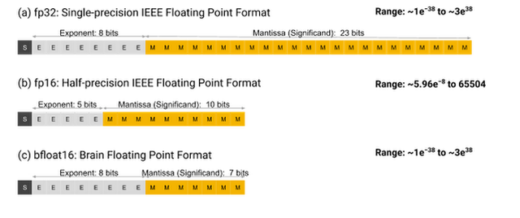
As artificial intelligence research needed higher performance floating point processing, Google Brain invented BF16, which is a 16-bit object, configured thus:
- 1-bit sign
- 8-bit exponent
- 7-bit mantissa
This gives essentially the same dynamic range as fp32, with reduced precision. Conversion from fp32 is very straightforward. Tests have shown that, despite the reduced precision, most AI applications perform very well at the expected increased speed.
In recent years, other solutions to this challenge have been proposed, which include fixed-point approaches, where all the numbers in a set have a common exponent value. But BF16 looks to be winning out.

