Judging distance

Sometimes I think that I fully understand something, but then I have doubts. I have been reflecting on something very everyday and simple: how we judge distance.

We all know how to assess a distance. You just need to look and you intuitively have an idea how far away something is. The question is: how do your brain/eyes arrive at this information …

Most animals have two eyes. They may be set in either side of the head, like a horse, which provides all-round vision, which is ideal for a herbivore that needs to keep a good lookout for movement indicating the approach of a predator. Other animals, like homo sapiens, have eyes set in the front of the head looking forward, which provide stereoscopic vision.

There is a myth that we see in 3D. This is no more true that the myth that “3D” movies are actually 3-dimensional [I wrote about this myth a while ago]. When an image is viewed [with a camera or an eye] it has a plane of focus, with a degree of sharpness in front and behind that plane [this is the “depth of field”]. The plane can be moved to focus on stuff nearer to or further away from the viewer. Having two eyes means that the brain has two images to work with. This is stereoscopic vision and gives an impression of depth and helps us estimate distances.

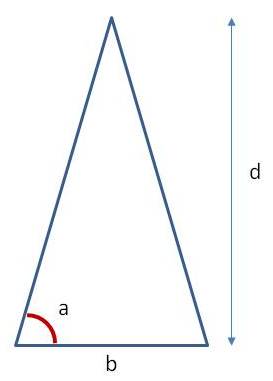But how does this actually work? I had always assumed that the geometry was quite simple, as shown in this diagram. The distance to the object is d and the space between the eyes is b. Each eye turns in to an angle of a so that the brain can calculate:

d = tan(a) * b / 2

I now have my doubts. I starting thinking about this when I was explaining to someone about the fact that each of us has a “leading” eye [which I wrote about here]. You can test yourself by looking at a slightly distant object with both eyes and pointing at it with a finger. While keeping your finger steady, shut one eye; if the finger is still aligned, that the open eye is your dominant one. If it is not still aligned, you will find that the other eye will show it lined up perfectly.

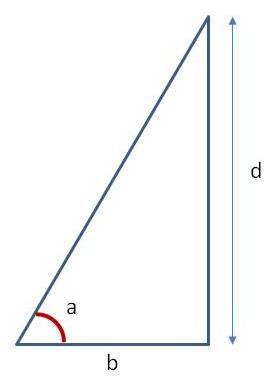This leads me to rethink the geometry, which I believe actually works like this diagram. One eye [the dominant one] looks directly at the object and the other is moved to an angle of a. The calculation is now:

d = tan(a) * b

Intuitively I feel that this should lead to a more accurate answer, as the full width between the eyes is being used. But I feel unable to justify this. Can anyone help? Does anyone know better? Comments or email are always welcome.

BTW, when I have ideas like this, I like to write them down before doing lots of research. My feeling is that I could quickly become “polluted” by other ideas and lose my own thread.