Organically Grown 3D Printable Heatsinks – Part 2: Trunks and Branches
Adrian Bejan’s Constructal Law states: “For a finite-size system to persist in time (to live), it must evolve in such a way that it provides easier access to the imposed currents that flow through it.” This can be seen at play in both animate and inanimate systems, from trees to lighting, from river systems to lungs. Such persistent systems tend to carry something between a volume and point. Lightning-electricity, trees-water, lungs-air, rivers-water. A heatsink is no exception. Taking heat from a point to a volume, or inversely taking cold from a volume to quench a point of heat. ‘Evolving in such a way that it provides easier access…’ is at the heart of the additive design process.
The iterative procedure to grow the heatsink geometry:
- Start with a minimal section of heatsink base, a thin sliver.
- Simulate to see how hot it gets
- Where its surface is hottest ‘grow’ the geometry there by a very small amount
- GoTo 2
- Repeat until a design space has been filled
is actually slightly more refined. If the addition of a small piece of geometry leads to an increase in heatsink base temperature (or not a substantial enough decrease), then that piece of geometry is removed and that location marked so as not to add there subsequently. The next hottest location is then considered, and so on.
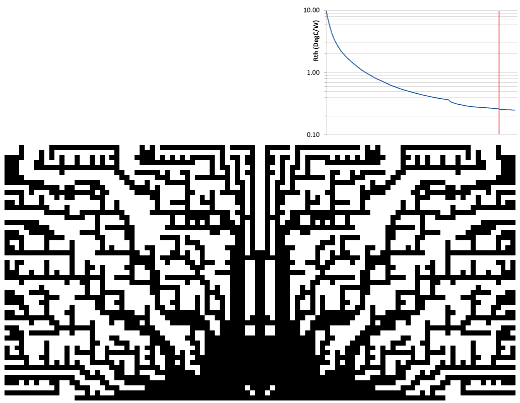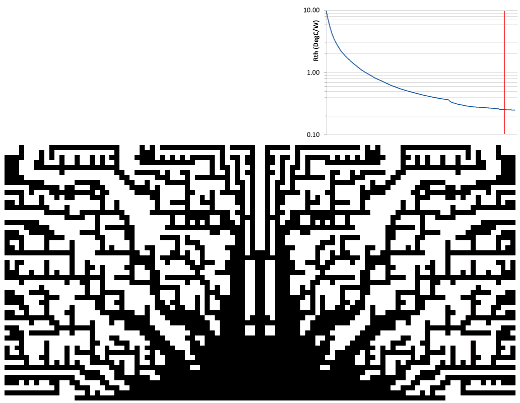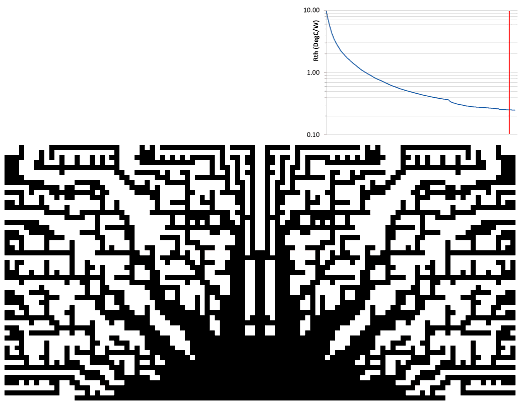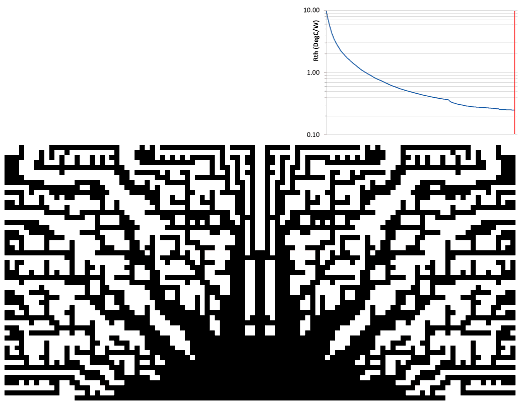
The end of the first year of growth occurred when no geometry could be added anywhere without extending beyond the design space, or causing an increase in base temperature. For the second year of growth, all those location that were marked as being detrimental were cleared and the iterative process repeated afresh.
A large surface area was achieved in the spindly growth of the first year. The second year saw a large ‘trunk’ develop that facilitated the flow of heat to the outer extremities. ‘Evolving in such a way that it provides easier access…’
The third year of growth further enhanced this flow of heat by thickening out ‘branches’ between the ‘trunk’ and the outer ‘leaves'(?)
It’s worth noting that the resulting complexity is a function of just a very basic set of growth criteria instructions. In much the same way that a seed is an instruction set for the consumption and conversion of local matter and energy into the resulting tree.
“Mighty oaks from little acorns grow”
No further reduction in growth could be achieved in subsequent years of trying. The additive process ended. That isn’t the end of the story though. The stepped nature of the geometry, due to the choice of the additive geometry shape, had opportunity to be further refined. More on chamfering in the next blog in this series.
25th March 2015, Ross-on-Wye.
