“All models are wrong, but some are useful” Part IV

The penultimate issue in this series of ‘reasons why an electronics cooling model can be wrong, but hey it’s fine as it will never be perfect but if you take some precautions it will always be useful, Parts 1, 2, 3 ….4, 5’ (Ian Dury, you have nothing to fear) focusses on the representation of PCBs (or PWBs if you are so inclined). Devilishly complex in their construction, deceptively simple in their use of only (nearly always) two materials, these little blighters pose some genuine challenges when ensuring that their representation in the CFD thermal model behaves accurately.

[Many of the concepts covered here you can see in this recorded webinar given last year]

Remember those thermal resistances I’ve been banging on about? It’s about time I explained exactly how they are defined. When looking at conduction (heat flow in solids) a thermal resistance =

d/kA

Where d is the length the heat has to flow, k is the thermal conductivity of the material (glass low, copper high) and A is the cross sectional area the heat has to squeeze through. There are analogies here to electronics, the electronic–hydraulic analogy covers the link between electronics, hydraulics and thermal. If you’re already versed in one discipline such an analogy should enable you to jump ship quite easily. So, what makes for a low  thermal resistance? If k or A are large that always help conductive heat removal. A high thermal conductivity will enable heat to travel much more easily through it without resulting in a temperature backup (rise). If the surface area of a hot object is large this also aids the removal of that heat, just ask an elephant on a hot day, go on, whisper in their large ear. Reducing d, the distance the heat has to flow to a colder ambient, is the most intuitive.

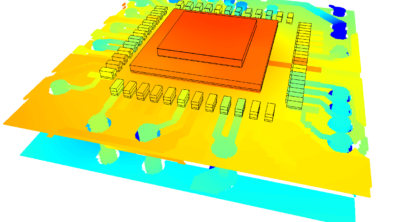
A PCB is most often made of FR4 and Copper. Thermal conductivity of FR4=~0.3 (W/mK), Cu = ~400 (W/mK), about 3 orders of magnitude different. In one respect very different, you’d expect heat would rather go anywhere but through the FR4. However, compared to the anaologous difference in electrical conductivity that has about 15 orders of magnitude difference between FR4 and Cu leading to electrical current flowing exclusively through the copper, heat flows through both FR4 (with difficulty) and Cu (with ease). As such the PCB, from a thermal perspective, has to be able to represent the effects of both contributors, including their 3D distribution. Or so you might think….

Modelling the PCB in all it’s glorious highly complex 3D detail will have penalties, especially in grid count and resulting solution times (hours not minutes). It would be good to not have to go to that level of detail if at all possible, without compromising solution accuracy of course.  Here we go, back to the core competence of a thermal ‘modeller’, the ability to create a tractable model representation that will provide thermal predictions in time scales bound by the industrial design environment they work in, but a prediction that is nevertheless still usefully accurate. So, what range of PCB thermal representations are there available and when should each be used?

The simplest representation is a 2D solid ‘plate’. Historically such reps were emplyed due to the severe computational limitation on number of grid cells using computer hardware of 15 years ago. If all you’re doing is air flow partioning and distribution simulation studies then a 2D rep is good enough (unless the thickness of the cards is important in terms of pressure drop blockage effects in a small pitch card rack). Often such studies don’t even include thermal effects so the issue of PCB thermal conductivity representation is moot.

The next level of detail is to model the PCB as a single 3D cuboidal object with a single thermal conductivity representative of the combined effects of the presence of both Cu and FR4. The simplest of conducting 3D models. FloTHERM and FloTHERM.PCB are intelligent enough to assign an appropriate orthotropic conductivity (different values in different directions, specifically different values for through-plane (Z direction) compared to in-plane (X=Y) directions). Such an approach will go some way to resolve the fact that the interspersed dielectric layers will result in an overall greater thermal resistance (e.g. reduced thermal conductivity) for heat that passes down through the board compared to the relative ease by which heat spreads in-plane. All you need to specify is something about the layer stack-up or %Cu in the board. Accuracy will be maintained when there is a uniform-ish distribution of heat on the surface of the board as such a single orthotropic approach doesn’t deal very well with local heat spreading from a small point source of heat.

Next level up is to represent the individual layers of the stack-up explicitly as cuboidal objects, again each with their own orthotropic conductivities. This will improve accuracy when there is significant heat spreading from small high powered components. The continued approach though of using a single orthotropic thermal conductivity assumes that the distribution of Cu/FR4 on that layer is itself pretty constant with no locally large areas of only Cu or only FR4. Grid count goes up significantly as you now need as many grid cells through the thickness of the board as there are layers, big ouch for a multi layer board with upwards of 14 layers.

State of the art is to represent the variation in thermal resistance both through the board as before but now also to model its variation in the plane of each layer. Unlike the previous 3D approaches where knowledge of the total % Cu was sufficient (+ the assumption that the distribution of the Cu/FR4 was uniform), this highly detailed approach necessitates the import of the routing artwork from the PCB design tool into FloTHERM or FloTHERM.PCB. Not possible with legacy methods of interfacing, i.e. the IDF file format, direct interfaces are required to suck the data out. Good news is that these are freely available with both of our CFD based thermal analysis products!

Even for this most detailed of reps the Cu features are not resolved exactly, the grid count to accommodate each and every trace, pad, fill etc. to exactly the right size is mind boggling (we laughed at the concept of solving  1,000,000 cell CFD models in a few hours a few years ago. We’re not laughing now, that’s for sure). Instead each layer is subdivided into an array of tessellated patches, each with their own orthotropic conductivity to represent the very local distribution of Cu/FR4 in that area.

You’ll get the best assured accuracy with this approach but it’s only worth going to this level of detail when you really need it. When’s that then? Simple, when the PCB is part of the critical/dominant heat flow path. True for natural convection environments (no fan blowing the air, air moving due to buoyancy alone). Here the heat would rather go through the board as the air is doing such a bad job at giving it an easy exit route. Very true for conduction cooled environments where the PCB is designed to be tightly joined to its big cold metal chassis.

One final word about these types of highly detailed models. Taking such a detailed approach for the PCB obliges you to take the same level of detail for the other parts on the critical heat flow path, especially components. If you’re modelling your components as blocks, that inaccuracy will swamp the advantage of modelling the PCB in detail. You’re obliged to model the components in detail or as CTMs. As with life, it’s always good practice to take a balanced approach to things.

[Many of the concepts covered here you can see in this recorded webinar given last year]

12th June, Ross-on-Wye