Exploring the quantum frontiers of differential equations in engineering

Intro

Differential equations offer valuable insight into fluid dynamics, heat transfer, structural mechanics and other pivotal domains, by capturing the fundamental relationships between variables and their change rates. This makes them indispensable instruments for understanding and forecasting the behavior of complex systems. Therefore, when it comes to engineering, solving these differential equations is crucial as it offers a robust mathematical toolset allowing them to model various physical phenomena.

CFD + Numerics

Computational Fluid Dynamics (CFD), in particular, empowers engineers to model and assess fluid dynamics within a simulated environment, offering them valuable predictions and insights crucial for making informed product design choices across various industries. These virtual replicas unlock unprecedented opportunities for refining processes, predicting system responses and enhancing decision-making.

Traditionally, when solving differential equations in CFD, several numerical techniques and methods are employed, with the most used being Finite Difference/Volume/Element methods. These involve discretizing the fluid domain into a grid or mesh, effectively converting the continuous partial differential equations (PDEs) governing fluid flow into a set of algebraic or ordinary differential equations, which then can be solved directly or iteratively. The accuracy and efficiency of these numerical techniques are paramount for achieving reliable results in CFD simulations. However, their effectiveness heavily depends on the size and resolution of the chosen discretization.

In many industrially relevant scenarios, such as scale-resolving turbulence simulations, computational complexity strains, existing computing resources and demands substantial power and time.

Method

In recent years, there has been a surge of interest in exploring the potential of quantum algorithms to improve the computational efficiency of solving partial differential equations. Shifting towards quantum architectures offers several advantages, including the potential for accelerating computations of targeted problems and leveraging the classically inaccessible sizes of the solution space that can be traversed before converging to an approximate problem’s solution(s).

In a joint study [1], researchers from the University of Exeter, PASQAL and Siemens Digital Industries Software investigated the implementation of iterative PDE solvers on quantum computers. Iterative solvers rely on converting the original PDE into a linear algebra problem (Ax=b), which is then solved iteratively until convergence, see Fig. 1. The primary computational hurdle lies in diagonalizing the remaining matrix A. Numerous quantum strategies have been proposed to address this challenge, each with different requirements for the underlying quantum hardware. For example, some methods promise exponential speed-ups in matrix inversion operations, albeit at the expense of requiring a fully fault-tolerant architecture [2].

Beyond the quantum-enabled advantages, iterative methods offer the additional prospect of reducing circuit depth compared to alternative quantum approaches targeting linear algebraic speedups, while still retaining better robustness than variational methods, which are renowned for their adaptability to noisy quantum devices. Consequently, quantum iterative methods appear to be promising candidates for architectures integrating near-term quantum error correction mechanisms.

The study outlines the intricacies involved in implementing a quantum method based on Jacobi iterations [5]. Drawing from existing techniques such as the Linear Combination of Unitaries [3], this proposal suggests new strategies for executing addition/subtraction operations within a quantum adaptation of iterative schemes.

Results

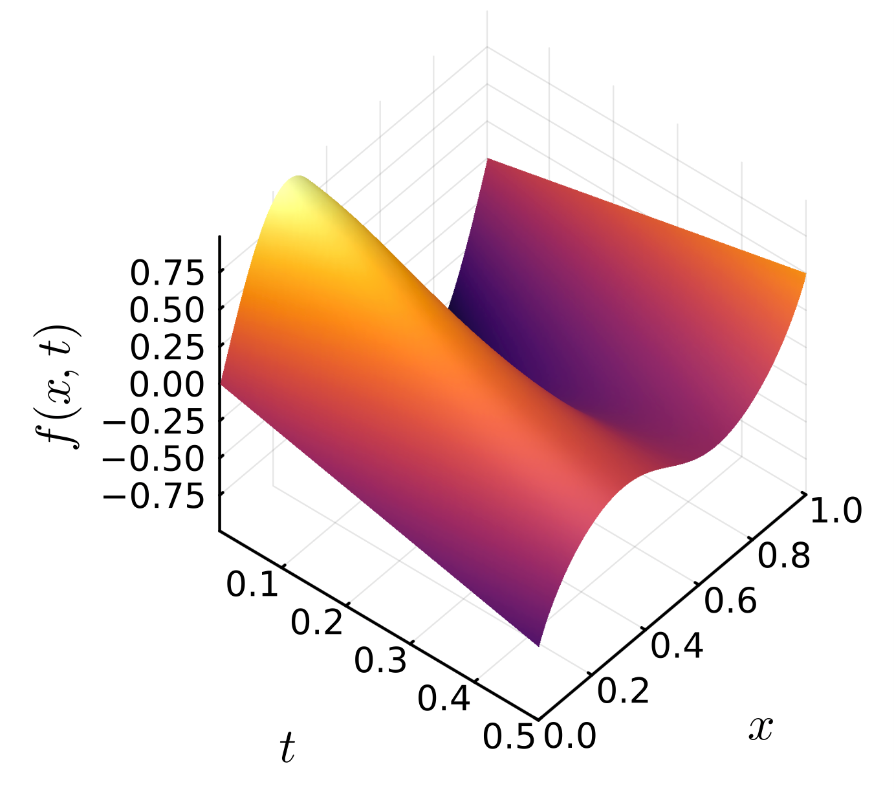
The results of the study show how the quantum Jacobi method achieves convergence comparable to its classical counterpart [5]. Convergence is reached within the same number of iterations, without meeting memory limitations typically associated with manipulating data and matrices in classical architectures. We exemplify in Fig. 2 the successful resolution of the Burgers equation with the new quantum iterative method, as a surface plot.

Conclusion

Overall, the most important observations underscore how the quantum Jacobi method achieves convergence comparable to its classical counterpart, meaning it requires the same number of iterations while unlocking the quantum advantage in overcoming memory limitations inherent in classical architectures handling large data or matrices.

The requirements on the quantum circuit in the study emphasize how quantum iterative methods can bridge the gap between near-term variational approaches and long-term algorithms, demanding sophisticated error correction to be implementable. Although beyond the capabilities of today’s technology, the resource estimates outlined in the paper are well aligned with the advancements in error-corrected quantum devices, as foreseen by the most recent hardware roadmaps [3]. Quantum iterative methods thus hold promising prospects for tackling instances of PDE numerical resolution, that classically pose significant challenges. The authors of the project already look forward to further work on optimizing quantum iterative approaches by complementing them with multi-grid algorithms and (quantum) machine learning tools, in order to improve performances and tackle more ambitious use cases with similar, realistic quantum computational resources.

References

1. Siemens Collaborates with Pasqal to Research Quantum Applications in Computer Aided Engineering, Simulation and Testing – PASQAL
2. Biamonte, Jacob, et al. “Quantum machine learning.” Nature 549.7671 (2017): 195-202.
3. Oszmaniec, Michał, et al. “Creating a superposition of unknown quantum states.” Physical review letters 116.11 (2016): 110403.
4. PASQAL Announces New Roadmap Focused on Business Utility and Scaling Beyond 1,000 Qubits Towards Fault Tolerance Era – PASQAL
5. Chelsea A. Williams, et al. “Quantum Iterative Methods for Solving Differential Equations with Application to Computational Fluid Dynamics”,arXiv:2404.08605, (2024)