Domestic Hot Water Heating, ‘Wat-er’ Waste of Energy. Part 2: Warm-up
Sure, most modern homes have much more advanced water heating systems than a big tank with an electric heater element. Systems that work on ‘point of use’ heating concepts that heat the water as it is being delivered, not heating up a large storage container for later use. One day I hope to live in such a house! Until then I’m going to worry and fret about the amount of money spent on heating water and subsequently the amount of money lost as that energy leaks away. So, can simulation predict how much money it takes to heat a water tank? Well yes!
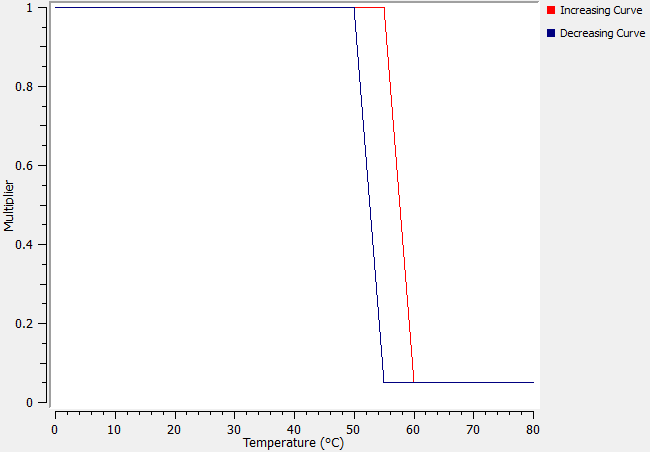Basic thermostatic control approaches relate the amount of (heating) power to the difference between a set point temperature and the temperature of the system being heated. This type of proportional control can be further enhanced to also take into account the rate at which the temperature is changing (derivative) as well as some history of what how the system has changed up to now (integral). Such PID control systems require constants that need to be tuned to achieve the most efficient approach to ensuring the set point temperature is achieved without under or over shoots. For this study I’ve adopted just a proportional control but including the effects of hysteresis using standard transient features in FloTHERM.
A maximum power (in this case 2000W) is derated once a nominated point in the tank exceeds 55 degC. Once it exceeds 60degC the power is limited to 100W. If the temperature starts to drop then a different curve is used to determine the required increase in power. This offset between the two is intended to stop rapid changes to the power as the water temperature tends towards its intended set point.
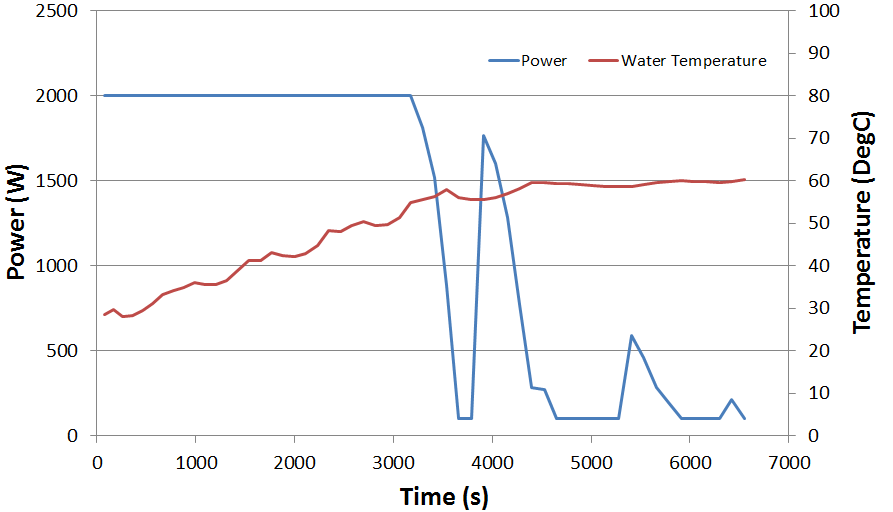The FloTHERM transient simulation covers a period of about 2 hours, during which the temperature is seen to stabilise at ~60degC. It takes just over an hour to settle down to this value. The changing power over that time is also stored.
Power is energy per time. The integral of the power history is the amount of energy (Joules) used. We pay for Joules, Joules = $£. About 7,800,000 Joules are used to raise the water temperature from 25 to 60 degC.
Does that sound about right? There’s a simple hand calculation that can also be used to double check: This 60 litre tank contains 60kg of water. The specific heat of water is ~ 4200 J/kgK. It takes 4200 Joules to raise 1kg of water 1 K (a 1 Kelvin increase is the same as a 1 degC increase). So, it will take 60*4200*(60-25) Joules to raise the entire tank to the required level. This works out at 8,820,000 Joules.
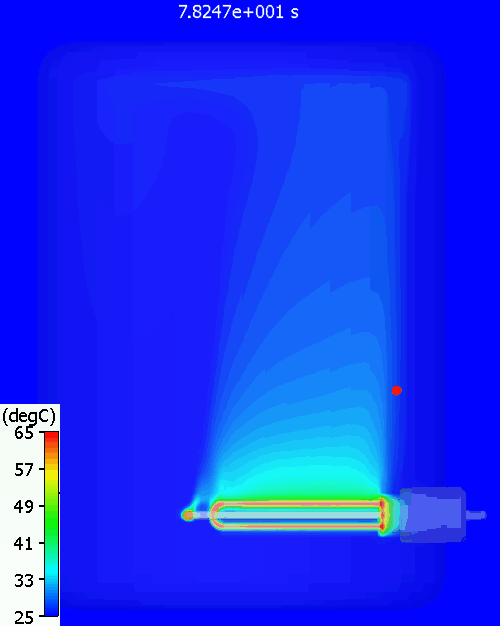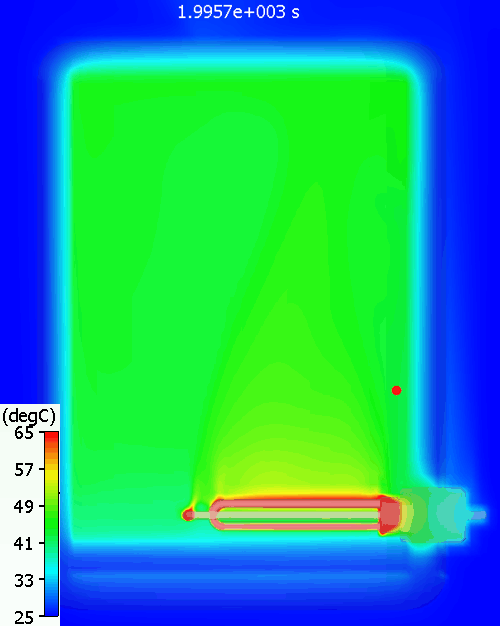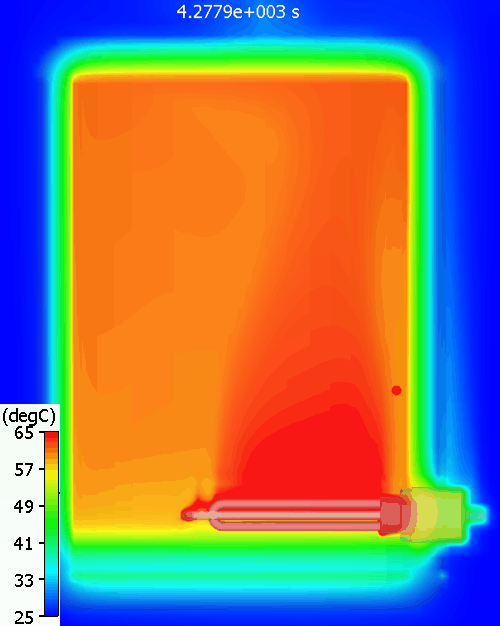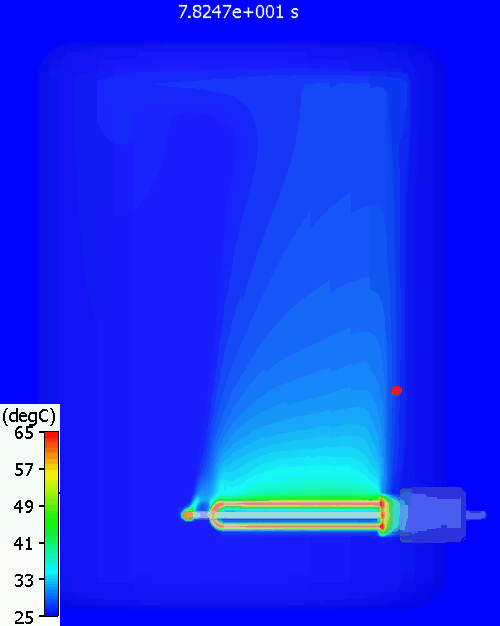
A bit higher than the simulation predicts. Why might that be? Let’s have a look at the temperature distribution within the tank during warm up:
The red dot is the point at which the water temperature is measured. As can be seen there is quite a variation in water temperature, it does not heat up equally throughout. As is often the case with such simple approaches, the hand calc used above assumes that the water heats up uniformly, just as doesn’t happen in reality. The 11% or so difference between hand calc and 3D CFD simulation is due to the fact that not all the water is heated to achieve the 60degC at the single thermostat control point, less energy is required. You can see a pool of much colder water at the bottom of the tank.
A good example of the value of 3D simulation over simpler assumption prone equations.
Next time we’ll look at how good the tank is at holding onto those 7.8 million Joules.
19th December 2014. Ross-on-Wye.
(p.s. tagged with ‘electronics cooling’ as for sure the water is doing its best to cool the electrically heated element just as much as the element is battling to heat the water 🙂 )
